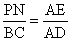2021年人教版 九年级数学下册第27章《相似》27.2.3 相似三角形应用举例
一、单选题
1.如图,小刚同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条边DF= 50 cm,EF= 30 cm,测得边DF离地面的高度1.5 m,CD=20 m,则树高AB为( )
A.12m
B.13.5 m
C.15m
D.16.5 m
2.如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE==20m,EC=10m,CD=20m,则河的宽度AB等于( )
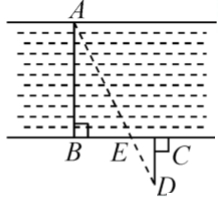
A.60m
B.40m
C.30m
D.20m
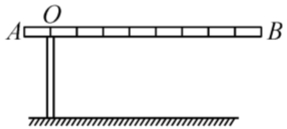
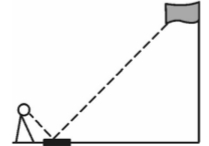
3.如图,小强在地面上放了一个平面镜,他站在合适的位置,刚好在平面镜中看到旗杆的顶部,此时小强与平面镜的水平距离为2m,旗杆底部与平面镜的水平距离为16m.若小强的眼睛与地面的距离为1.5m,则旗杆的高度为( )
A.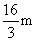
B.9m
C.12m
D.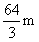
二、填空题
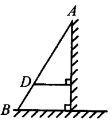
1.如图, AB是斜靠在墙壁上的长梯,梯脚B距墙1.6m,梯上点D距墙1.4m,BD长0.55m,则梯子的长为m.
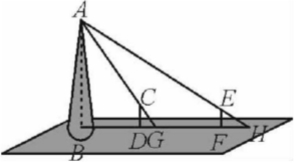
2.如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2m的标杆CD和EF,两标杆相隔52 m,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2m到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆EF后退4 m到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高是m.
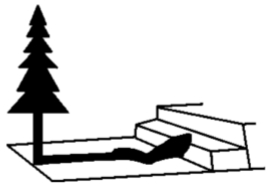
3.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1 m的竹竿的影长为0.4 m,同时另--名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得台阶上影子长为0.2 m,一级台阶高为0.3 m,如图所示,若此时落在地面上的影长为4.4 m,则树高为m.
4.测量不能到达顶部的物体的高度,通常借助太阳光照射物体形成影子,根据同一时刻物高与影长或利用相似三角形来解决问题.
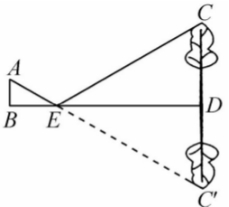
5.如图,身高为1.7 m的小明AB站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C'D,A,E,C'在一条视线上,已知河BD的宽度为12 m,BE=3 m,则树CD的高为m.
三、解答题
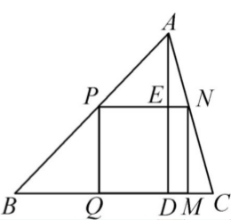
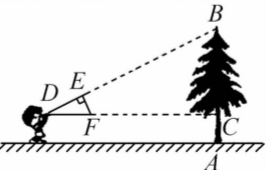
如图,△ABC是一块锐角三角形余料,边BC= 120 mm,高AD= 80mm,要把它加工成正方形零件,使一边在BC上,其余两个顶点分别在边AB,AC上,那么这个正方形的边长是多少?