引导语

    “数和式”是刻画现实世界中数量关系的数学模型，从整式到分式，如同从整数到分数一样，都是源于现实世界的客观需要．现在，我们就来研究分式。

做一做

    1.一项工程，甲施工队5天可以完成。甲施工队每天完成的工程量是多少？3天完成的工程量又是多少？如果乙施工队a天可以完成这项工程，那么乙施工队每天完成的工程量是多少？b（b

    甲施工队每天完成的工程量是

    3天完成的工程量

    乙施工队每天完成的工程量是

    b（b

    2.已知甲、乙两地之间的路程为m km.如果A车的速度为n km/h，B车比A车每小时多行20 km，那么从甲地到乙地，A车和B车所用的时间各为多少？

    从甲地到乙地，A车和B车所用的时间 .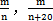

大家谈谈

    由上面的问题，我们分别得到下面一些代数式：

    ，；，，.

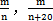    将这些代数式按“分母”含与不含字母来分类，可分成怎样的两类？

    一般地，我们把形如的代数式叫做分式(fraction)，其中，A，B都是整式，且B含有字母．A叫做分式的分子，B叫做分式的分母.

例1 指出下列各式中，哪些是整式，哪些是分式.

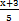x-2，，5x2，，，，.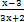

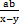解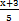： x-2，，5x2，都是整式；

     因为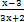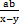，，的分母都含有字母，所以它们都是分式.

    在分数中，分母不能等于0．同样，在分式中，分母也不能等于0，即当分式的分母等于0时，分式没有意义，如分式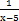.，当x-5≠0，即x≠5时，它有意义;当x-5=0，即x=5时，它没有意义.

    在什么情况下，下了各分式无意义？

    ，，.

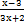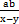例2 

   当y取什么值时，分式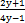 的值是零？

解：①使得分式的值为0，则2y+1=0

      ∴y =-1/2

    ②使得分式有意义，则4y-1≠0 

     ∴把y=-1/2代入4y-1=-3≠0

     ∴当y=-1/2时，此分式的值是零。

观察与思考

    分数的分子和分母同乘(或除以)一个不等于0的数，其值不变．如

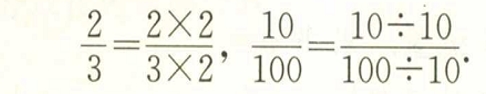
    类比分数的这种性质，思考:分式的分子和分母同乘(或除以)一个不等于0的整式，分式的值会怎样？

分数的基本性质

    分式的分子和分母同乘（或除以）一个不等于0的整式，分式的值不变.

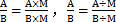    . 期中，M是不等于0的整式.

小结

    分式的定义：整式A、B相除可写为的形式，若分母中含有字母，那么叫做分式。

    分式的意义：分母≠0

    分式的值为0： ①分子=0  ②代入分母≠0  ③最后答案