课程内容
九年级数学上册第3章《对圆的进一步认识》3.3 圆周角(第一课时)
第三章《对圆的进一步认识》
3.3 圆周角
第一课时
观察与思考
(1)如图3-22,点A,B,C是⊙O上的三个点.以A为端点作射线AB,AC,得到了一个怎样的角?
(2)(1)中是∠BAC有什么特征?
∠BAC的顶点在圆上,并且它的两边在圆内的部分是圆的两条弦,像这样的角叫做圆周角(angle in circular segment).
(3)圆周角与圆心角有什么不同?
(4)观察图3-23中的各角,其中哪些是圆周角?哪些是圆心角?
实验与探究
任意画一个⊙O,在圆上任意取三个点A,B,C,连接AB,AC.
(1)圆心0与∠BAC有几种可能的位置关系?与同学交流.
圆心与同圆上的圆周角的位置关系有三种情况:圆心在圆周角的一边上(图3-24①),圆心在圆周角的内部(
图3-24②),圆心在圆周角的外部(图3-24③).
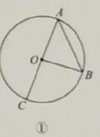
(2)在图3-24①中,AB是⊙O的直径,连接OC,你发现∠BOC与∠BAC有什么位置和数量关系?
(3)能将问题(2)中的结论推广到图3-24②③吗?由此你猜想圆周角与它所对弧上的圆心角有怎样的数量关系?怎样证明你的结论?
已知:如图3-25,A,B,C是⊙O上的任意一定.
求证:∠BAC=1/2∠BOC.
证明
(1)当圆心O在∠BAC的一条边上时(图3-25①).
在△OAB中,
∵OA=OB,
∴∠BAO=∠OBA.
∵∠BOC=∠BAO+∠OBA,
∴∠BOC=2∠BAO.
∴∠BAC=1/2∠BOC.
(2)当圆心O在∠BAC的内部时,作直径AD(图3-25②).
(3)当圆心O在∠BAC的外部时(图3-25③),你能给出证明吗?试一试,与同学交流.
归纳以上三种情况的结论,就得到
圆周角定理
圆周角等于它所对弧上的圆心角的一半.
因为圆心角与它所对弧的度数相等,因而由圆周角定理可以直接得到
推论1 圆周角的度数等于它所对弧的度数的一半.
例1
如图3-26,在⊙O中,∠AOB=110°,在点C在

上,求∠ACB的度数.
解
点C在的位置有两种情况:
(1)当点C在劣弧上时(图3-26①),
∵∠AOB=110°,
∴
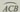
的度数=110°.
∴

的度数=360°-110°=250°.
∴∠ACB=1/2×250°=125°.
(2)当点C在优弧上时(图3-26②),
∵∠AOB=110°,
∴∠ACB=1/2∠AOB
=1/2×110°=55°.
练习
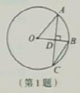
1.如图,在⊙O中,∠AOB=70°,OB⊥AC,垂足为点D,求∠OBC的度数.
2.已知△ABC内接于⊙O,AB=AC,且

的度数为130°,求∠A的度数.
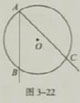


 上,求∠ACB的度数.
上,求∠ACB的度数.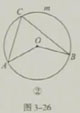
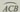 的度数=110°.
的度数=110°. 的度数=360°-110°=250°.
的度数=360°-110°=250°.
 的度数为130°,求∠A的度数.
的度数为130°,求∠A的度数.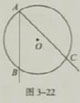




 上,求∠ACB的度数.
上,求∠ACB的度数.
 的度数=110°.
的度数=110°. 的度数=360°-110°=250°.
的度数=360°-110°=250°.


 的度数为130°,求∠A的度数.
的度数为130°,求∠A的度数.