课程内容
三年级数学下册《期中整理与复习》
我学到了什么
在第一单元《除法》中,我学到了:
1、两、三位数除以一位数的笔算。
2、确定商是几位数。
3、连除和乘除混合运算。
一、两、三位数除以一位数的笔算;
1、从高位算起,先算百位,再算十位,最后算个位。如果百位不够除要先看被除数的前两位。
2、除到哪一位商写在哪一位的上面。
3、余数要比除数小。
4、十位和个位上如果不够商1的写0占位。
二、确定商是几位数:
被除数的百位上的数字比除数大或等于除数,商就是三位数。被除数百位上的数字比除数小商就是两位数。
三、连除和乘除混合运算:
1、只有乘除法,按从左向右的运算顺序。
2、有括号的,要先算括号里面的。
我学到了什么?
小军:今天8头奶牛共产奶184千克。
小丽:平均每头奶牛产奶多少千克?
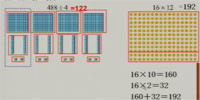
184÷8的商是几位数?你能用竖式计算出结果吗?并说说竖式每一步的意思。
在第二单元《图形的运动》中,我学到了:
1、轴对称图形判断和制作。
2、平移和旋转。
3、会在方格纸上判断图形的运动的情况,并会做相应的运动后的图形。
轴对称图形的特点:
沿中间对折,左右或上下两边能完全重合。中间的折痕所在的直线就是对称轴。
平移现象:沿着某一条直线运动。在运动中大小、形状、方向都不改变。
旋转现象:围绕一个中心点转动。在转动中大小、形状不变;方向改变。
描述一物体平移现象:
找图形平移前后的一对对应点,这一对应点的移动情况就是图形的运动情况。
做平移后的图形:找出图形的关键点,移动每个关键点,然后连线。
结合上图说一说,什么样的图形是轴对称图形?生活中有哪些平移现象和旋转现象?
在第三单元《乘法》中,我学到了:
1、因数是整十数乘法的口算。
2、两位数乘两位数的口算方法。
3、两位数乘两位数的估算方法。
4、两位数乘两位数的笔算方法。
因数是整十数乘法的口算
先计算末尾0前面数字的乘法,然后在所得积后面添上被省略的0.
一个因数不变,另一个因数乘积,积就乘几。
两位数乘两位数的口算方法
(1)转化法14×12=14×6×2;把其中的一个因数分成两个一位数,用连乘法计算。
(2)分解法14×12=14×10+14×2:把其中的一个因数分成一个整十数和一个一位数,用另一个因数分别与这两个数先乘,再把积相加。
(3)表格法14×12=(10+4)×(10+2):把两个因数都分解成一个整十数和一个一位数,两个两个相乘,再把4个积相加。
两位数乘两位数的估算方法
估算时,把算式中的两个或一个因数看成接近于它的整十的数,再口算出大约是多少。这样可以快速估出的数的大致范围。
两位数乘两位数的笔算方法(不进位)
列竖式计算两位数乘两位数时,先用第二个因数个位上的数去乘第一个因数的各个数位上的数,得数的末位和第二个因数个位上的数位对齐,再用第二个因数十位上的数去乘第一个因数的各个数位上的数,得数是多少个”十“,个位上的0可以省略不写,所以得数的末位和第二个因数十位对齐,然后把两次乘得的积相加。
两位数乘两位数的笔算方法(有进位)
列竖式时,末位对齐,先用第二个因数个位上的数去乘第一个因数的各个数位上的数,用哪一位的数去乘得,得数的末位就和哪一位的数对齐,哪一位的数上的乘积满几十,就要向前一位进几十,最后把每次乘得的积相加。
我的成长足迹
小军:我最喜欢用画图的方法解决问题,因为图最具体。
小花:我知道很多美丽的图案都是轴对称图形。
小雷:我喜欢用点子图计算乘法,它让我明白了竖式的每一步的意思。
小林:先估算,再计算,我的错误就少多啦!
我提出的问题
巩固应用
1.圈一圈,算一算。
2.说一说,算一算。
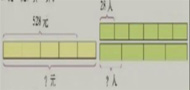
528÷4×5 28×6÷4
=132×5 =168÷4
=660(元) =42(人)