课程内容
《集合的含义与表示》
1、我们以前已经接触过的集合
·自然数集合;
·到角的两边的距离相等的所有点的集合,是角平分线。
2、集合的含义
(1)1到20以内的所有质数;
(2)我国从1991到2003年的13年内所发射的所有人造卫星。
(3)到直线l的距离等于定长d所有的点;
(4)方程x2+3x-2=0的所有实数根;
一般地,我们把研究对象统称为元素,把一些元素组成的总体叫做集合(简称集)。
3、集合中元素的特征
(1)确定性
(2)互异性
(3)无序性
例子:
(1)A={1,3},问3,5哪个是A的元素?
(2)B={素质好的人}能否表示成为集合?
(3)C={2,2,4}表示是否正确?
(4)D={太平洋,大西洋}
E={大西洋,太平洋}
集合D,E是不是表示相同的集合?
4、元素与集合之间的关系
·如果a是集合A中的元素,就说a属于集合A,记作a∈A;
·如果a不是集合A中的元素,就说a不属于集合A,记作a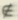 A;
A;
5、常用的数集及其记法
我们通常用大写拉丁字母A,B,C…表示集合,用小写拉丁字母a,b,c…表示集合中的元素。
·全体非负整数组成的集合称为自然数集,记为N。
·所有正整数组成的集合称为正整数集,记为N′或N。
·全体整数组成的集合称为整数集,记为Z。
·全体有理数组成的集合称为有理数集,记为Q。
·全体实数组成的集合称为实数集,记为R。
6、集合的表示方法
(1)列举法:把集合中的元素一一列出来,写在大括号内的表示集合的方法。
例:用列举法表示下列集合:
①方程x2=x的所有实数根组成的集合。
②由1-20以内的所有质数组成的集合。
(2)描述法——用集合所含元素的共同特征表示集合的方法。
具体方法:在花括号内先写上表示这个集合元素的一般符号及取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征。
描述法表示集合的基本模式是:
{元素的一般符号及取值范围|元素所具有的性质}
(3)图示法——画一条封闭曲线,用它的内部来表示一个集合,常用于表示不需给具体元素的抽象集合,对已给出了具体元素的集合也当然可以用图示法来表示,这种图称为Venn图。
反馈演练
1、填空题。
(1)现有:①不大于√3的正有理数②我校高一年级所有高个子同学③全部长方形④全体无实根的一元二次方程,四个条件中所指对象不能组成集合的_____。
(2)设集合A={-2,-1,0,1,2},B={x∈A时代数式x2-1的值},则B中的元素是_____。
2、选择题
(1)以下说法正确的是( )
A、“实数集”可记为{R}或{实数集}
B、{a,b,c,d}与{c,d,b,a}是两个不同的集合
C、“我校高一年级全体数学学得好的同学”不能组成一个集合,因为其元素不确定
(2)已知2是集合M={0,a,a2-3a+2}中的元素,则实数a为( )
A、2 B、0或3 C、3 D、0、2、3均可
思考1:a与{a}的含义是否相同?
思考2:集合{1,2}与集合{(1,2)}相同吗?
思考3:集合{y|y=x2,x∈R}与集合{y=x2}相同吗?
思考4:集合{(x,y)|y=x2,x∈R}的几何意义如何?
3、用适当的方法表示下列集合。
(1)绝对值小于3的所有整数组成的集合;
(2)所有奇数组成的集合;
(3)由数字1,2,3组成的所有三位数构成的集合。
4、用列举法表示下列集合:
(1)A={x∈Z|4/(x-3)∈Z};
(2){(x,y)|x+y=3,x∈N,y∈N}。
5、设集合A={5,|a+1|,2a+1},已知3∈A,求实数a的值。
6、已知集合A={1,2,3},B={1,2},设集合C={x|x=a-b,a∈A,b∈B},试用列举法表示集合C。











