课程内容
第25章《概率初步》25.1 随机事件与概率(2)
本课是在学生已经学习了随机事件概念以及定性判断随机事件发生的可能性大小的基础上,给出了从定量的角度去刻画随机事件发生可能性大小的概念——概率,并求一些简单随机事件的概率。
学习目标:
1、概率的意义;
2、计算一些简单随机事件的概率。
学习重点:
概率的意义。
复习:下列事件中哪些事件是随机事件?哪些事件是必然事件?哪些是不可能事件?
(1)抛出的铅球会下落
(2)某运动员百米赛跑的成绩为2秒
(3)买到的电影票,座位号为单号
(4)x2+1是正数
(5)投掷硬币时,国徽朝上
概率的起源
——都是骰子惹的“祸”
三四百年前在欧洲许多国家,贵族之间盛行赌博之风。掷骰子是他们常用的一种赌博方式。
柯尔莫哥洛夫,俄国著名的数学家,主要研究概率论、算法信息论、拓扑学、直觉主义逻辑、湍流、经典力学和计算复杂性理论,最为人所道的是对概率论公理化所作出的贡献。他曾说:“概率论作为数学学科可以而且应该从公理开始建设,和几何、代数的路一样”。
1、认识概率
问题:在上节课的问题2中,掷一枚六个面上分别刻有1到6的点数的骰子,向上一面上出现的点数有几种可能?每种点数出现的可能性大小是多少?
一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记为P(A)。
2、如何求概率
问题:在问题1和问题2的试验中,有哪些共同特点?
(1)每一次试验中,可能出现的结果只有有限个;
(2)每一次试验中,各种结果出现的可能性相等。
问题:在问题1中,你能求出“抽到偶数”、“抽到奇数”这两个事件的概率吗?对于具有上述特点的试验,如何求某事件的概率?
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率P(A)=m/n。
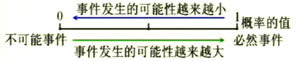
问题:根据上述求概率的方法,事件A发生的概率取值范围是怎样的?
0≤P(A)≤1
3、求概率
例1:掷一枚质地均匀的骰子,观察向上一面的点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2且小于5。
练习1:抛掷1枚质地均匀的硬币,向上一面有几种可能的结果?它们的可能性相等吗?由此能得到“正面向上”的概率吗?
练习2:把一幅普通扑克牌中的13张黑桃牌洗匀后正面向下放在桌子上,从中随机抽取一张,求下列事件的概率:
(1)抽出的牌是黑桃6;
(2)抽出的牌是黑桃10;
(3)抽出的牌带有人像;
(4)抽出的牌上的数小于5;
(5)抽出的牌的花色是黑桃。
能力拓展
盒中有x枚黑棋和y枚白棋,这些棋除颜色外无其他差别。
(1)从盒中随机取出一枚棋子,如果它是黑棋的概率是3/8,写出表示x和y关系的表达式。
(2)往盒中再放进10枚黑棋,取得黑棋的概率变为1/2,求x和y的值。