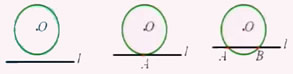
| 直线和圆的位置关系 | 相交 | 相切 | 相离 |
| 图形 | 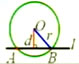 |
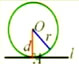 |
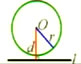 |
| 公共点个数 | 2个 | 1个 | 没有 |
| 公共点名称 | 交点 | 切点 | — |
| 直线名称 | 割线 | 切线 | — |
| 距离d与半径r的关系 | d<r | d=r | d>r |

| 直线和圆的位置关系 | 相交 | 相切 | 相离 |
| 图形 |  |
 |
 |
| 公共点个数 | 2个 | 1个 | 没有 |
| 公共点名称 | 交点 | 切点 | — |
| 直线名称 | 割线 | 切线 | — |
| 距离d与半径r的关系 | d<r | d=r | d>r |
评论2
点此登录 后即可畅所欲言
[贵州省遵义市] 666666,好

tz040410
2018-11-26 21:49:54
[湖北省襄阳市] 点个赞 分享 收藏 手机观看 扫码下载同桌100APP 在手机上观看学习视频更轻松! 留言 同步课程 课程内容 第24章《圆》24.2.2 直线和圆的位置关系(1) 1、情景引入 2、直线和圆的位置关系(图形特征) 直线和圆没有公共点时,叫做直线和圆相离。 直线和圆有唯一公共点时,叫做直线和圆相切。 这条直线叫做圆的切线,这个点叫做切点。 直线和圆有两个公共点时,叫做直线和圆相交。 1、能否根据基本概念判断直线和圆的位置关系? 直线l和⊙O没有公共点 ←→ 直线l和⊙O相离 直线l和⊙O只有一个公共点 ←→ 直线l和⊙O相切 直线l和⊙O有两个公共点 ←→ 直线l和⊙O相交 用公共点的个数来判断直线和圆的位置关系。 2、是否还有其他的方法判断直线和圆的位置关系? 2、直线和圆的位置关系(数量特征) 当直线和圆相离、相切、相交时,d与r有何关系? 1、直线和圆相离 ←→ d>r; 2、直线和圆相切 ←→ d=r; 3、直线和圆相交 ←→ d<r。 直线和圆的位置关系的识别与特征: 小结:利用圆心到直线的距离与半径的大小关系来识别直线和圆的位置关系。 3、归纳小结 直线和圆的位置关系 相交 相切 相离 图形 公共点个数 2个 1个 没有 公共点名称 交点 切点 — 直线名称 割线 切线 — 距离d与半径r的关系 d<r d=r d>r 4、练习 练习1:圆的直径是13cm,如果直线和圆心的距离分别是①4.5cm;②6.5cm;③8cm,那么直线和圆分别是什么位置关系?有几个公共点? 练习2:已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与x轴的位置关系是______,⊙A与y轴的位置关系是______。 例:Rt△ABC,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么? (1)r=2cm;(2)r=2.4cm;(3)r=3cm。 分析: 根据直线和圆的位置关系的数量特征,应该用圆心到直线的距离d与半径r的大小进行比较; 关键是确定圆心C到直线AB的距离d,这个距离是多少呢?怎么求这个距离? 练习3:己知⊙O到直线l的距离为d,⊙O的半径为r,若d、r是方程x2-7x 12=0的两个根,则直线l和⊙O的位置关系是______。 5、课堂小结 1、直线和圆的位置关系有三种:相离、相切和相交。 2、识别直线和圆的位置关系的方法: (1)一种是根据定义进行识别: 直线l和⊙O没有公共点 ←→ 直线l和⊙O相离 直线l和⊙O只有一个公共点 ←→ 直线l和⊙O相切 直线l和⊙O有两个公共点 ←→ 直线l和⊙O相交 (2)另一种是根据圆心到直线的距离d与圆半径r的大小关系来进行识别: d>r ←→ 直线l和⊙O相离 d=r ←→ 直线l和⊙O相切 d<r ←→ 直线l和⊙O相交 精彩评论

138****2412
2016-08-19 11:30:49