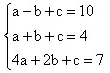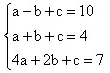课程内容
第22章《二次函数》22.1 二次函数的图象和性质(7)
确定二次函数的解析式
学习目标:
会用待定系数法确定二次函数y=ax2+bx+c的解析式。
学习重点:
二次函数y=ax2+bx+c解析式的确定。
1、复习确定一次函数解析式的方法
已知一次函数图象上的几个点可以求出它的解析式?利用了怎样的方法?
2、探究确定二次函数解析式的方法
类比确定一次函数解析式的方法,如果一个二次函数的图象经过(-1,10),(1,4),(2,7)三点,试求出这个二次函数的解析式。
设所求二次函数为y=ax2+bx+c。
由函数图象经过(-1,10),(1,4),(2,7)三点,得关于a,b,c的三元一次方程组
解这个方程组,得
a=2,b=-3,c=5
所求的二次函数是y=2x2-3x+5
刚才我们通过己知图象上的三点确定了二次函数的解析式,如果只知道图象上任意两点是否可以确定解析式?
如果知道图象的顶点和图象上另一点,能否确定解析式呢?
一个二次函数图象的顶点为(1,-4),图象又过点(2,-3)。
(1)求这个二次函数的解析式。
(2)求该函数的图象与坐标轴的交点坐标。
解:∵图象的顶点为(1,-4)
∴设所求二次函数为y=a(x-1)2-4
∵函数图象经过点(2,-3)
∴可列方程a(2-1)2-4=-3
解得a=1
∴所求的二次函数是y=(x-1)2-4
即y=x2-2x-3
2、练习,巩固所学二次函数内容
问题3
根据下列条件,求出二次函数的解析式。
(1)图象经过(-1,1),(1,3),(0,1)三点;
(2)图象的顶点为(-1,-8),且过点(0,-6);
(3)图象经过(3,0),(2,-3)两点,并且以x=1为对称轴;
(4)图象经过一次函数y=-x+3图象与坐标轴的两个交点,并且经过点(1,1)。
3、运用性质,巩固练习
(5)已知二次函数y=ax2+bx-4的图象经过(-1,-5),(1,1)两点,求这个二次函数的解析式。