课程内容：

《平行四边形（2）》
复习：平行四边形的性质：
    平行四边形的对边平行，平行四边形的对边相等。平行四边形的对角相等。平行四边形的邻角互补。
例题：如图，◇ABCD的对角线，AC、BD相交于点O。线段OA与OC、OB与OD有何数量关系？
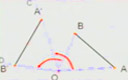
练习：如图，把两张完全相同的平行四边形纸片叠合在一起，在它们的中心O钉一个图钉，将一个平行四边形绕O旋转180°，你发现了什么？
定义：◇ABCD绕它的中心O旋转180°，后与自身重合，这时我们说◇ABCD是中心对称图形，点O是它的对称中心。
例题：已知：如图，◇ABCD的对角线AC、BD相较于点O。求证：OA=OC，OB=OD。
平行四边形的性质：平行四边形的对角线互相平分。
例1.已知如下图，在◇ABCD中，AC与BD相交于点O，点E、F在AC上，且BE∥DF。求证：BE=DF。
例2.如图，四边形ABCD是平行四边形，AB=10，AD=8，AC⊥BC，求BC、CD、AC、OA的长以及◇ABCD的面积。
性质运用于再探究：◇ABCD的对角线AC与BD相较于O，直线EF过点O与AB、CD分别相交于E、F，试探究OE与OF的大小关系并说明理由。在上述问题中，若直线EF绕点O旋转与边DA、BC的延长线交于点E、F，上述结论是否仍然成立？试说明理由。在上述问题中，若将直线EF绕点O旋转至下图的位置时，上述结论是否仍然成立？
练习：
1.平行四边形的一边长为5cm，则它的对角线可能是（  ）
    A.4cm和6cm    B.4cm和14cm    C.4cm和8cm    D.10cm和2cm
2.在平行四边形ABCD中，EF过对角线的交点O，若AB=4，BC=7，OE=3，则四边形EFCD周长是（  ）
    A.14    B.11    C.10    D.17
思考后解决：
1.已知：◇ABCD的对角线AC、BD相交于点O，AC=16cm，BD=12cm，BC=10cm，则◇ABCD的周长是______________。◇ABCD的面积是_______________。
2.如图，EF过◇ABCD的对角线AC、BD的交点O，△AOE与△COF的面积有何关系？四边形AEFD与四边形BCFE的面积有何关系？
3.小亮家有一块平行四边形的苹果园，爸爸想在中间留一条小路，把它分成面积相等的两块，请你帮小亮的爸爸想想办法，可以怎么分？