《图形的旋转》
1、什么是图形的旋转？
旋转的定义：在平面内，将一个图形绕一个定点按某个方向转动一定的角度，这样的图形运动叫做图形的旋转。这个定点叫做旋转中心，转动的角度叫做旋转角。
2、旋转前后，图形的形状、大小、位置是否发生变化？旋转变换有什么特征？
操作1、将三角板ABC绕点C按逆时针方向旋转到DEC的位置，旋转前、后三角形的位置改变了吗？形状、大小改变了吗？
度量∠ACD与∠BCE的度数，线段AC与DC、BC与EC的长度，你发现了什么？
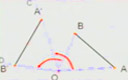
操作2：将△ABC绕点O按顺时针方向旋转到△A′B′C′的位置，度量∠AOA′、∠BOB′与∠COC′的度数，线段AO与A′O、BO与B′O、CO与C′O的长度，你发现了什么？
旋转前、后的图形全等。对应点到旋转中心的距离相等；每一对对应点与旋转中心的连线所成的角彼此相等。
考考你
1、已知线段AB和点O，画出AB绕点O逆时针旋转100°后的图形。
小结：如何按要求作出简单平面图形旋转后的图形？
作图的步骤：
（1）确定旋转中心、旋转方向和旋转角。
（2）在已知图形上找一些关键点
（3）作出这些关键点的对应点
（4）顺次连接这些对应点
作图关键：旋转中心、旋转方向、旋转角度、旋转的对应点。
2、如图，画出△ABC绕点C按顺时针方向旋转120°后的对应的三角形。
3、香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成，它是由其中一个瓣经过几次旋转得到的？
紫荆花图案绕中心旋转多少度后能和原来的图案互相重合？
例题讲解
例题1：如图，E是正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形。
变式：如图，正方形ABCD中，E是CD边上任意一点，将三角形ADE顺时针旋转，得到三角形ABF。
（1）旋转中心是哪一点？
（2）旋转了多少度？
（3）点M是AD的中点，经上述旋转后，点M到什么位置？
（4）连结EF，△AEF是什么三角形？
（5）若正方形ABCD的边长是2，
     ①则点M在旋转时经过的路径长是多少？
     ②求四边形AFCE的面积。
课堂小结
这节课，主要学习了什么？
1、确定一个图形旋转后的位置的条件：
（1）图形原来的位置
（2）旋转中心
（3）旋转方向和旋转角
2、利用旋转的基本性质作出简单平面图形旋转后的图形。