课程内容

《线段的垂直平分线》（2）
线段垂直平分线的性质定理：
    线段垂直平分线上的点到这条线段的两个端点的距离相等。
数学语言：
  ∵EF⊥AB  AO=BO
    （或EF垂直平分AB）
    点P在EF上
  ∴PA=PB
请写出上面定理的逆命题
线段垂直平分线上的点到这条线段的两个端点的距离相等。
如果一个点在一条线段的垂直平分线上，那么这个点到这条线段的两个端点的距离相等。
如果一个点到一条线段的两个端点的距离相等，那么这个点在这条线段垂直平分线上。
填写下面命题证明过程的理由：
已知：如图，P为线段AB外的一点，且PA=PB。
求证，点P在线段AB的垂直平分线上。
证明：过点P作直线EF⊥AB，垂足为O，则
   ∠POA=∠POB=90°（垂直定义）
   在Rt△PAO和Rt△PBO中，
   PA=PB（已知），PO=PO（公共边）
   ∴Rt△PAO≌Rt△PBO（HL）
   ∴AO=BO（全等三角形的对应相等）
   ∴EF是线段AB的垂直平分线（线段垂直平分线的定义）
   ∴点P在线段AB的垂直平分线上。
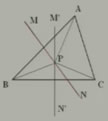
例1 已知，如图，在△ABC中，边AB，BC的垂直平分线交于P。
求证：PA=PB=PC。

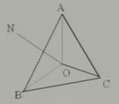
例2 已知：在△ABC中，ON是AB的垂直平分线，OA=OC。
求证：点O在BC的垂直平分线上。

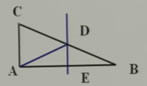
例3 在△ABC中，DE垂直平分AB，AB=8cm，△ACD的周长为10cm。求△ABC的周长。

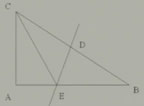
例4 如图：在Rt△ABC中，∠A=90°，线段BC的垂直平分线DE，如果CE恰好是∠ACB的平分线，求∠B的度数。

例5 如图：AB=AD，BC=DC，E是AC一点。
    求证：BE=DE。

试一试
方便居民的生活，市政府计划在三个住宅小区A、B、C之间修建一个购物中心，试问，该购物中心应建于何处，才能使得它到三个小区的距离相等。
实际问题→数学化
求作一点P，使它和△ABC的三个顶点距离相等。
求作：作线段AB的垂直平分线。
作法：
1、分别以点A和B为圆心，以大于AB/2长为半径作弧，两弧交于点C和D。
2、作直线CD。
则直线CD就是线段AB的垂直平分线。
请你说明CD为什么是AB的垂直平分线，并与同伴进行交流。