课程内容
《线段的垂直平分线》(1)
线段垂直平分线的性质:
线段垂直平分线上的点到这条线段的两个端点的距离相等。
已知:线段AB,直线EF⊥AB,垂足为O,AO=BO,点P是EF上异于点O的任意一点。
求证:PA=PB。
证明:∵EF⊥AB(已知),
∴∠POA=∠POB=90°(垂直的定义)
在△PAO和△PBO中,
AO=BO(已知)
∠POA=∠POB(已证)
PO=PO(公共边)
∴△PAO≌△PBO(SAS)
∴PA=PB
线段垂直平分线的性质定理:
线段垂直平分线上的点到这条线段的两个端点的距离相等。
数学语言:
∵EF⊥AB AO=BO
(或EF垂直平分AB)
点P在EF上
∴PA=PB
线段垂直平分线的性质定理的应用
例 已知,如图在Rt△ABC中,∠A=90°,AB=3,AC=5,BC的垂直平分线DE交BC于点D,交AC于点E,求△ABE的周长。
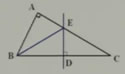
解:∵DE垂直平分BC
∴BE=CE
∴△ABE的周长
=AB+AE+BE
=AB+AE+EC
=AB+AC
=3+5
=8
练习:已知:如图,在△ABC中,AC=25,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长为48,求BC的长。
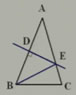
练习:已知:如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F,且∠BAC=115°,求∠EAF的度数。
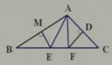
请写出上面定理的逆命题
线段垂直平分线上的点到这条线段的两个端点的距离相等。
如果一个点在一条线段的垂直平分线上,那么这个点到这条线段的两个端点的距离相等。
如果一个点到一条线段的两个端点的距离相等,那么这个点在这条线段垂直平分线上。




























