课程内容:
《等腰三角形》
回顾:△ABC有什么特点?
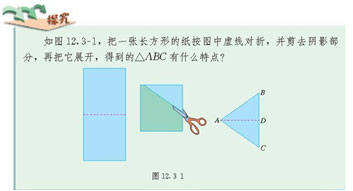
思考:1.等腰三角形是轴对称图形吗?
2.将等腰三角形沿折痕对折,你发现了哪些重合的线段和角?
猜想与论证:
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC。 求证:∠B=∠C。
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
等腰三角形性质1:
等腰三角形的两个底角相等。(等边对等角)。
大胆猜想:等腰三角形除了两底角相等以外,你还能发现它的其他性质吗?
等腰三角形性质2:
等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合。(简称“三线合一”)。
知识应用:
1.等腰三角形的一个底角为80°,它的另外两个角为______。
2.等腰三角形一个内角为75°,它的另外两个角为______。
3.等腰三角形一个内角为100°,它的另外两个角为______。
4.等腰三角形的一个外角为100°,它的另外两个角为______。
填空:根据等腰三角形性质2,在△ABC中,AB=AC时,
(1)∵AD是角平分线 ∴____⊥____,____=____。
(2)∵AD是中线, ∴____⊥____,∠____=∠____。
(3)∵AD⊥BC,∴∠____=∠____,____=____。
例1.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
例2.已知:如图,房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC,求顶架上∠B、∠C、∠BAD、∠CAD的度数。
知识巩固:
已知:如图,AB=AC,DB=DC,问:AD与BC是什么关系?
小结:

此内容正在抓紧时间编辑中,请耐心等待
王老师
男,中教高级职称
从事了多年的教学工作,积累了丰富的教学经验。教学风格幽默风趣,善于根据学生的思路进行恰当的引导。
























