课程内容
《平行线的性质》
合作学习
任意画两条互相平行的直线,再任意画一条直线与这两条平行线相交。测量同位角的度数,你发现了什么?与其他同学的发现相同吗?
一般地,平行线有下面的性质:两条平行直线被第三条直线所截,同位角相等。
简单地说,两直线平行,同位角相等。
例1 如图,梯子的各条横档互相平行,∠1=100°,求∠2的度数。

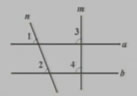
例2 如图,已知∠1=∠2,若直线b⊥m,则直线a⊥m,请说明理由。
作业题
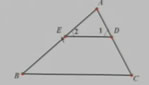
2、如图,D,E分别是AC,AB上的点。已知∠1=60°,∠C=60°,∠2=40°。
(1)DE与BC平行吗?请说明理由。
(2)求∠B的度数。
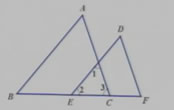
3、如图,∠B=∠2,∠F=∠3,点B,E,C,F在同一条直线上,请找出图中的平行线,并说明∠A=∠1=∠D的理由。
4、折叠三角形纸片ABC,使点A落在BC上的点F,且折痕DE∥BC,若∠B=50°,求∠BDF的度数,并说明理由。
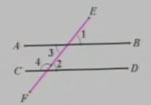
如图,直线AB∥CD,并被直线EF所截。∠2与∠3相等吗?∠3与∠4的和是多少度?
建议从以下几方面思考:
(1)回顾我们已知道的平行线的性质,由此能得出图中哪一对角相等?
(2)∠3与∠1有什么关系?∠4与∠2呢?
你发现平行线还有哪些性质?
一般地,平行线还有下面的性质:两条平行直线被第三条直线所截,内错角相等。简单地说,两直线平行,内错角相等。
两条平行直线被第三条直线所截,同旁内角互补。简单地说,两直线平行,同旁内角互补。
例3 如图,已知AB∥CD,AD∥BC,判断该∠1与∠2是否相等,并说明理由。
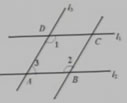
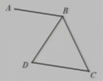
例4 如图,已知∠ABC+∠C=180°,BD平分∠ABC,∠CBD与∠D相等吗?请说明理由。
练习
2、如图,已知AB∥CD,AD∥BC,填空:
(1)∵AB∥CD(已知),
∴∠1=______(两直线平行,内错角相等);
(1)∵AD∥BC(已知),
∴∠2=______( )。
3、如图,已知AD∥BC,∠BAD=∠BCD。请说明AB与CD平行的理由。
4、如图,D是BC上的一点,DE∥AB,交AC于点E,DF∥AC,交AB于点F。若∠A=60°,求∠FDE的度数。
5、一艘船从O处出发,沿北偏东60°方向行驶至A,然后向正东方向行驶至C后又改变航向,朝与出发时相反的方向行驶至B处,请画出该船的航线示意图,并求∠ACB的度数。
6、如图,已知BC∥AD,将线段CD作怎样的平移交换,使图形出现一对全等三角形?请画出经变换后的图形,并说明理由。
全课总结:
1、平行线有什么性质?
2、解题方法上你有什么收获?
























