课程内容
《频率的稳定性》(1)
小明和小丽在玩抛图钉游戏
抛掷一枚图钉,落地后会出现两种情况:钉尖朝上,钉尖朝下。你认为钉尖朝上和钉尖朝下的可能性一样大吗?
直觉告诉我任意掷一枚图钉,钉尖朝上和钉尖朝下的可能性是不相同的。
我的直觉跟你一样,但我不知道对不对。
不妨让我们用试验来验证吧!
活动一:做一做
(1)两人一组做20次掷图钉游戏,并将数据记录在下表中:
| 试验总次数 | |
| 钉尖朝上次数 | |
| 钉尖朝下次数 | |
| 钉尖朝上频率(钉尖朝上次数/试验总次数) | |
| 钉尖朝下频率(钉尖朝下次数/试验总次数) |
(2)累计全班同学的实验结果,并将试验数据汇总填入下表:
| 试验总次数n | 20 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
| 钉尖朝上次数m | |||||||||||
| 钉尖朝上频率m/n |
(4)小明共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,观察图像,钉尖朝上的频率的变化有什么规律?

结论:
在试验次数很大时,钉尖朝上的频率都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性。
活动二:议一议
(1)通过上面的试验,你认为钉尖朝上和钉尖朝下的可能性一样大吗?你是怎样想的?
(2)小明和小丽一起做了1000次掷图钉的试验,其中有640次钉尖朝上。据此,他们认为钉尖朝上的可能性比钉尖朝下的可能性大。你同意他们的说法吗?
数学史实
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律。这是频率稳定性定理。
频率的稳定性是由瑞士数学家雅布·伯努利(1654-1705)最早阐明的,他还提出了由频率可以估计事件发生的可能性大小。
活动三:练一练
1、某林业部门要考查某种幼树在一定条件下的移植成活率,应采用什么具体做法?
在同样条件下,大量地对这种幼树进行移植并统计成活情况,计算成活的频率。如果随着移植棵数的越来越大,频率越来越稳定于某个常数,那么这个常数就可以被当作成活率的近似值。
(1)下表是统计试验中的部分数据,请补充完整:
| 移植总数 | 成活率 | 成活的频率 |
| 10 | 8 | 0.8 |
| 50 | 47 | 0.94 |
| 270 | 235 | 0.870 |
| 400 | 369 | 0.923 |
| 750 | 662 | 0.883 |
| 1500 | 1335 | 0.890 |
| 3500 | 3203 | 0.915 |
| 7000 | 6335 | 0.905 |
| 9000 | 8073 | 0.897 |
| 14000 | 12628 | 0.902 |
(3)林业部门种植了该幼树1000棵,估计能成活______棵。
(4)我们学校需种植这样的树苗500棵来绿化校园,则至少向林业部门购买约______棵。
3、某厂打算生产一种中学生使用的笔袋,但无法确定各种颜色的产量,于是该文具厂就笔袋的颜色随机调查了5000名中学生,并在调查到1000名、2000名、3000名、4000名、5000名时分别计算了各种颜色的频率,绘制折线图如下:
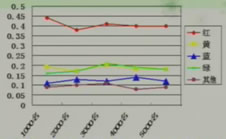
(1)随着调查次数的增加,红色的频率如何变化?
(2)你能估计调查到10000名同学时,红色的频率是多少吗?
(3)若你是该厂的负责人,你将如何安排生产各种颜色的产量?
数学理解
抛一个如图所示的瓶盖,盖口向上或盖口向下的可能性是否一样大?怎样才能验证自己结论的正确性?
课堂总结:
1、通过本节课的学习,你了解了哪些知识?
2、在本节课的教学活动中,你获得了哪些活动体验?




























