课程内容：

《单项式乘多项式法则的再认识——因式分解（一）》
复习回顾：计算下列各式：
    x（x+1）=__________；    （x+1）（x-1）=____________。
思考：630能被哪些数整除？说说你是怎样想的。
      630=2×3²×5×7
探究：请把下列多项式写成整式的乘积的形式：
    （1）x²+x=_________；    （2）x²-1=___________。
    上面我们把一个多项式化成了几个整式的积的形式，像这样的式子变形叫做把这个多项式因式分解，也叫做把这个多项式分解因式。

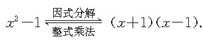
    因式分解与整式乘法是相反方向的变形。也可以称为它们互为逆运算。
    ma+mb+mc=m（a+b+c）
    它的各项都有一个公共的因式m，我们把因式m叫做这个多项式的公因式。由此可得：ma+mb+mc=m（a+b+c）这样就把ma+mb+mc分解成两个因式乘积的形式，其中一个因式是各项的公因式m，另一个因式（a+b+c）是ma+mb+mc除以m所得的商，像这种分解因式的方法叫做提公因式法。
例1.把8a³b²+12ab³c分解因式。
    观察方向：一看系数，二看字母，三看指数。
例2.把2a（b+c）-3（b+c）分解因式。
练习：判断下列各式哪些是整式乘法？哪些是因式分解？
    （1）x²-4y²=（x+2y）（x-2y）
    （2）2x（x-3y）=2x²-6xy
    （3）（5a²-1）²=25a²-10a+1
    （4）x²+4x+4=（x+2）²
    （5）（a-3）（a+3）=a²-9
    （6）m²-4=（m+2）（m-2）
    （7）2∏R+2∏r=2∏（R+r）
练习：说出下列多项式各项的公因式：
    （1）ma+mb；（2）4kx-8ky；（3）5y³+20y²；（4）a²b-2ab²+ab
试一试：把下列各式用提公因式法因式分解
    ①3mx-6my；②x²y+xy²；③12a²b³-8a³b²-16ab⁴
练习：1.把下列各式分解因式：
    （1）8m²n+2mn；          （2）12xyz-9x²y²；
    （3）2a（y-z）-3b（z-y）   （4）p（a²+b²）-q（a²+b²）
      2.先分解因式，再求值。
      4a²（x+7）-3（x+7），其中a=5，x=3。
      3.计算5×3⁴+24×3³+63×3²
练习：把下列各式分解因式。
    1.2a-4b；                   2.ax²+ax-4a；
    3.3ab²-3a²b；               4.2x³+2x²-6x；
    5.7x²+7x+14；               6.-12a²b+24ab²；
    7.xy-x²y²-x³y³；            8.27x³+9x²y。