课程内容：

《实数的概念（2）》
归纳：实数的大小比较
    当数从有理数扩充到实数以后，与有理数一样，对于数轴上的任意两个点，右边的点所表示的实数总比左边的点表示的实数大。
练习：比较大小
    1.3____5    2.√3____√5
    若a>0,b>0,且a²>b²,则a>b。
练习：比较下列各组数的大小：
    （1）√10    √5
    （2）√3     3
    （3）√16    4
    （4）√0.12    -√0.12
思考：1.怎样比较-√3与-√7的大小。
        两个负数绝对值大的反而小
      2.怎样比较0.5与√0.5的大小。
        可以用平方法，把两个整数都化成带根号或不带根号的式子，从而比较出它们的大小。
归纳：当数从有理数扩充到实数以后，有理数关于相反数和绝对值的意义同样适用于实数。即，实数的相反数、绝对值意义和有理数是一样的。
例：√2的相反数是_______；-∏的相反数是________；0的相反数是________。
    │√2│=______  ;│∏│= ______    │0│= ______
归纳：数a的相反数是-a（a表示任意一个实数）。一个正实数的绝对值是它本身；一个负实数的绝对值是它的相反数；0的绝对值是0。

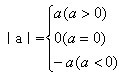
例1.
（1）分别求-√6、∏-3.14的相反数。
（2）指出-√5、1-_³√3各是什么数的相反数。
（3）求³√-64的绝对值；
（4）已知一个数的绝对值是√3，求这个数。
练习：
    1.a是一个实数，它的相反数为____;如果a≠0那么它的倒数为____。
    2.-√3的相反数是____,绝对值是____。
    3.1-√2的相反数是____,绝对值是____。
    4.³√-27的绝对值是____。
    5.已知一个数的绝对值是√5，则这个数是____。
    6.绝对值小于√6的整数有____。
归纳：当数从有理数扩充到实数以后，实数之间不仅可以进行加、减、乘、除（除数不为0）、乘方运算，而且正数及0可以进行开平方运算，任何一个实数可以进行开立方运算。在进行实数运算时，有理数的运算法则及运算性质等同样适用。
例2.计算下列各式的值：
    （1）（√3-√2）-√2    （2）3√3+2√3
归纳：在实数运算中，当遇到无理数并且需要求出结果的近似值时，可以按照所要求的精确度用相应的近似有限小数去代替无理数，再进行计算。
例。计算（结果保留小数点后两位）
（1）√5+∏    （2）√3·√2
练习：如图，A、B两点的坐标分别是A（1，√2）、B（√5，0），求△OAB的面积（精确到0.1）。