课程内容：

《实数的概念（1）》
探究：
归纳：事实上，任何一个有理数都可以化成有限小数或无限循环小数。反过来，任何有限小数或无限循环小数，都是有理数。
练习：前几节课，我们曾经把两个面积为1的小正方形沿对角线剪开，将所得的4个直角三角形拼在一起，就得到一个面积为2的大正方形。你知道这个大正方形的变长是多少吗？
     设大正方形的边长为x，则
     x₂=2    所以，根据算术平方根的意义可知
     x=√2

定义：很多数的平方根和立方根都是无限不循环小数，无限不循环小数又叫做无理数。有理数和无理数统称实数。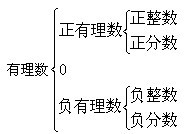
         

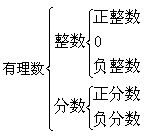
练习：把下列各数填入相应的集合内：
    ｜-√9｜  ^3√2  √81  3∏  0.7循环  -3/4  ^3√-9   6    3.14
（1）整数集合{    …}
（2）分数集合{    …}
（3）负数集合{    …}
（4）有理数集合{    …}
（5）无理数集合{    …}
（6）实数集合{    …}
思考：直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上的一点由原点到达点o'，点o'的坐标是多少？
归纳：实数与数轴上的点一一对应。即每一个实数都可以用数轴上的一个点来表示；反之，数轴上的每一点都表示一个实数。
      同样地，平面直角坐标系内的点与有序实数对是一一对应的。
练习：判断对错
    1.无理数都是无限小数。（  ）
    2.无限小数都是无理数。（  ）
    3.实数不是有理数就是无理数。（  ）
    4.带根号的数都是无理数。（  ）
    5.无理数一定都带根号。（  ）
    6.数轴上的任意一点都可以用实数表示。（  ）
    7.两个无理数之和一定是无理数。（  ）
我们的收获：
    ●学习了无理数和实数的概念
    ●实数的分类
    ●数轴上的点与实数的一一对应关系以及平面直角坐标系内的点与有序实数对也是一一对应的关系。