课程内容：

《反比例函数》
复习：
·变量，常量的概念
·自变量，函数
·函数的三种表达法
·一次函数（一般形式，图象特征及性质）
·一次函数的自变量取值范围都是全体实数。
思考：下列问题中，变量间的对应关系可以用怎样的函数关系表示？
1.京沪铁路全程为1463km，某此列车的平均速度为v（km/h）随此次列车的全程运行时间t（h）的变化而变化。
2.某住宅小区要种植一个面积为1000㎡的矩形草坪，草坪的长y（单位：m）随宽x（单位：m）的变化而变化。
3.已知北京市的总面积为1.68×10⁴平方千米，人均占有的土地面积s（单位：平方千米/人）随全市总人口n（单位：人）的变化而变化。
说一说：你还能举出生活中反比例函数的例子吗？每位同学找一个，与同桌交流。
练习：下列函数中哪些是反比例函数？哪些是一次函数？
例1.下列关系式中的y是x的反比例函数吗？如果是，比例系数k是多少？
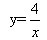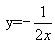    （1）    （2）    （3）y=1-x    （4）xy=1    （5）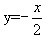
例2.已知y是x的反比例函数，当x=2时，y=6，（1）写出y与x的函数关系式；（2）求当x=4时y的值。
例3.y是x的反比例函数，下表给出了x与y的一些值。（1）写出这个反比例函数的表达式；（2）根据函数表达式完成上表。
例4.已知函数y=y₁+y₂，y₁与x成正比例，y₂与x成反比例，且当x=1时，y=4，当x=2时，y=5。（1）求y与x的函数关系；（2）当x=4时用的值是多少？
练习：已知y与x²成反比例，当x=3时，y=4,。（1）写出y与x的函数关系式；（2）求当x=1.5时y的值。