课程内容：

《有理数的加法（2）》
    同学们，想一想我们上节课所学过的内容，你还能回忆起有理数加法法则吗？
复习知识：同号两数相加，取相同的符号，并把绝对值相加。异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值。互为相反数的两个数相加得零。一个数与零相加，仍得这个数。
讨论：两个有理数相加，和是否一定大于每个加数？
做一做（一）：
（1）(-9.18)+6.18
（2）6.18+(-9.18)
（3）(-2.37)+(-4.63)
（4）(-4.63)+(-2.37)

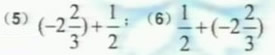
做一做（二）：
（1）[8+(-5)]+(-4)
（2）8+[(-5)+(-4)]
（3）[(-7)+(-10)]+(-11)
（4）(-7)+[(-10)+(-11)]
（5）[(-22)+(-27)]+(+27)
（6）(-22)+[(-27)+(+27)]
    通过以上的计算，你能从中发现什么规律？
概括：有理数的加法仍满足加法交换律和结合律。加法交换律：两个数相加，交换加数的位置，和不变。加法结合律：三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。
总结：三个或三个以上的有理数相加，可以任意交换加数的位置，也可以先把其中的几个数相加，使计算简化。
小结：有理数加法交换律和结合律的目的是什么？原则是什么？