课程内容
《相似三角形的性质》
研究三个三角形相似的判定问题，除了上述方法个，还可以通过与三角形全等的判定进行类比，得出有关猜想，例如，类比“三边对应相等，两三角形全等”，可以猜想：“三边对应成比例，两三角形相似”。
判定定理3 对于任意两个三角形，如果一个三角形的三边和另一个三角形的三边对应成比例，那么这两个三角形相似，简述为：三边对应成比例两三角形相似。
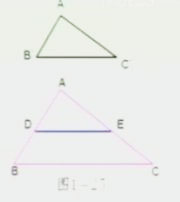
已知图1-25在△ABC和△A'B'C'中
A'B'/AB=B'C'/BC=C'A'/CA
求证：△A'B'C'∽△ABC
证明：在△ABC的边AB（或延长线）上截取AD=A'B'，过点D作DE∥BC，交AC于点E，于是可得
AD/AB=DE/BC=AE/AC，△ADE∽ABC，因为AD=A'B'，所以AD/AB=A'B'/AB又因为A'B'/AB=B'C'/BC=C'A'/CA，所以DE/BC=B'C'/BC，EA/CA=C'A'/CA，则DE=B'C'，EA=C'A'，故△ADE≌△A'B'C'，
因此△A'B'C'∽△ABC
例1如图1-26，已知D、E、F是△ABC三边BC、CA、AB的中点，求证△DEF∽△ABC
证明：因为线段EF、FD、DE是△ABC的中位线
所以EF=1/2BC，FD=1/2CA，DE=1/2AB，从而得EF/BC=FD/CA=DE/AB=1/2，则△DEF与△ABC的三边对应成比例，故△DEF∽△ABC。
我们知道，与一般三角形相比，直角三角形有一个角为直角，三边长满足勾股定理等特殊的边角关系这种关系，可以使判定两个直角三角形相似的条件得到简化，例如我们有
定理（1）如果两个直角有一个锐角对应相等，那么它们相似。
（2）如果两个直角形有一个锐角对应相等，那么它们相似；
此外与直角三角形全等的判定定理灯比，可引出直角三角形相似的另一个判定理。
定理 如果一个直角的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例，那么这两个三角形相似。
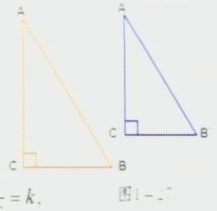
已知如图1-27Rt△ABC与Rt△A'B'C'中∠C=∠C'=90，AB/A'B'=AC/A'C'
求证：Rt△ABC∽Rt△A'B'C'
证明：由已知，可设AB/A'B/=AC/A'C'=k
那么AB=kA'C'，AC=kA'C'
所以BC=AB-AC=k(A'B'-A'C')=kB'C'，
即BC=kB'C'，所以±B/A'B/=AC/A'C'=BC/B'C'=k
由判定定理3得Rt△ABC∽Rt△A'B'C'
例5 如图1-28，已知AD，BE分别是△ABC中BC边和AC边上的高。H是AD、BE的交点
求证：（1）AD.BC=BE.AC
（2）AH.HD=BH.HE
证明：（1）在Rt△ADC和Rt△BEC中，因为∠ACD=∠BCE，所以Rt△ADC∽Rt△BECAD/BE=AC/BC，即AD.BC=BE=AC
（2）在Rt△AHE和Rt△BHD中，因为∠AHE=∠BHD,
所以Rt△AHE∽Rt△BHD，AH/BH=HE/HD，即AH.HD=BH.HE。
2、相似三角形的性质
我们知道，相似三角形的判定，讨论的是具备哪些条件。才能有两个三角形相似，相似三角形的性质讨论的则是在两个构型相似的条件，可以得出哪些结论，一般地，我们可以在两个三角形相似的条件下，考察与三角形相关的元素，如果两个三角形的高，周长、角平分线，中线、面积等所具有的关系。
可以发现下列相似三角形的性质定理
（1）相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比；
（2）相似三角形周长的比等于相似比；
（3）相似三角形面积的比等于相似比。
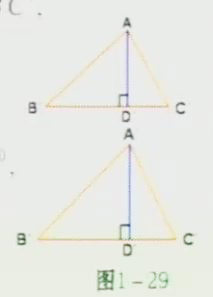
证明（1）如图1-29，△ABC∽△A'B'C'，设相似比为k，AD、A'D'分别是△ABC和△A'B'C对应边上的高因为△ABC∽△A'B'C'，所以∠B=∠B'，又因为∠ADB=A'D'B=90，
所以△ABD∽A'B'D'，
因此AD/A'D=AB/A'D'=k
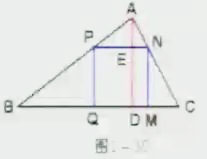
例6 如果1-30，锐角三角形ABC是一块钢板余料，边BC=24cm，BC边上的高AD=12cm，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB，AC上求这个正方形零件的边长。
解 正方形PQMN为加工成的正方形零件，边QM在BC上，顶点P、N、分别在AB、AC上，△ABC的高与边PN相交于点E设正方形的边长为xcm。
因为PN∥BC，所以△APN∽△ABC，
则AE/AD=PN/BC，即12-x/12=s/24,解得=8（cm）
思考 由相似三角形的性质定理可知相似三角形的高、中线、内角平分线，周长、面积等，要素与相似比有关，拓宽思路，考虑与三角形有关，但不在三角形内的其他元素，这些元素是否与三角形的相似比有联系，你想互了那些元素。
问题1 两个相似三角形的外接的直径比，周长比、面积比与相似比有什么关系？
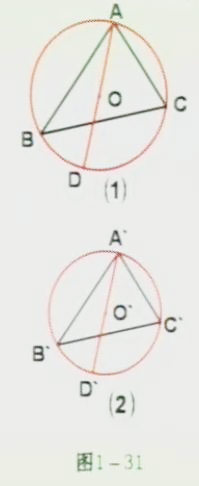
探究 如图1-31（1）、(2),△ABC∽△A'B'C'，AD、A'D'分别是△ABC和△A'B'C'外接的直径连接BD、B'D'，则∠ABD=∠A'B'C'=90
因为△ABC∽△A'B'C'，所以∠C=∠C'而∠D=∠C，∠D'=∠C'
所以∠D=∠D'
故△ABD∽A'B'D'
相似三角形外接的直径比，周长比等于相似比外接圆的面积比等于相似比有平方。
问题2 两个相似三角形的内切圆的直径比、周长比、面积比与相似比有什么关系？请同学们自己探究。
