课程内容

《平行线等分线段成比例定理》
我们看到，平行线等分线定理以“相邻两条平行线间的距离相等”为条件如果一组平行线中相邻两条平行线间距离不相等，又可以得出怎样的结论呢？
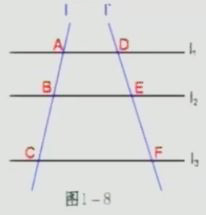
观察，如图1-8，两条直线被一组平行线所截，当平行线间的距离不相等时，所截的线段AB与BC与EF之间有什么关系？
容易发现，AB≠BC，DE≠EF
由以往学习平面几何的经验，当几何图形平全等时，可以考察它们是否相似，而相似是通过“对应边面比例，对应角相等”来表现的由此得到启发，我们可以研究被一组平行线截得的线段是否有“对应边顾比例”？
探究，在图1-8中AB︰BC=DE︰EF相等吗？取AB︰BC=2︰3的特殊情形进行探讨。

我们可以将上述问题化归为平行线间距离相等的情形。
如图1-9，如果AB︰BC=2︰3，设线段AB的中点为P1，线段BC的三分点为P2、P3这里有AP1=P2B=BP2=P2P3=P3C
分别过P1、P2、P3作直线，a1、a2、a3平行于L与L'的交点分别为Q1、Q2、Q3由平行线等分线段定理可知；
DQ1=Q1E=EQ2=Q2Q3=Q3F，因为
DE=DQ1+Q1E=2DQ1，EF=EQ2+Q2Q3+Q3F=3DQ1
所以DE︰EF=2DQ1︰3DQ1，因此AB︰BC=DE︰EF (1)
当AB/BC为有理数时，即AB、BC=m/n（m、n是互岳的正整数），AB是长度单位的m倍，BC是长度单位的n倍，依照上面的方法，可以证明（1）成立。更一般地，可以证明，当L∥L2∥L3，且AB/BC是实数时，（1）式也成立，由（1）式和比例性质，可以得到AB/BC =DE/EF,AB/AC=DE/DF,BC/AC=EF/DF
一般地，我们有
平行线分线段成比例定理：三条平行线截两条直线所截的对应线段成比例。
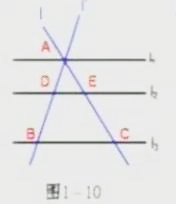
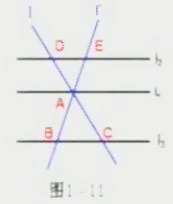
观察图1-10和1-11，它们是图1-8的特殊情形，即L与L'的交点都在L上，根据平行线分线段成比例定理，可得AD/AB=AE/AC。
如果把图1-10和图1-11中的直线L2看成是平行于△ABC的BC边的直线，那么可以得到；

推论：平行三角形一边的直线截其他两边（或两边的延长线）所得的对应线段成比例
例1 如图1-12，△ABC中，DE∥BC，DF∥AC，AE=4，EC=2，BC=8，求BF和CF的长
解 因为DE∥BC，所以
DA/AB=AE/AC=4/6=2/3  （1）
因为DF∥AC，所以AD/AB=CF/CB（2）
由（1）（2）式得2/3=CF/8,即CF=16/3，所以BF=8-6-16/=8/3
例2 如图1-13，△ABC中DE∥BC，EF∥CD，求证：AD是AB和AF的比例中项
证明 在△ABC中，因为DE∥BC，
所以AB/AD=AC/AE(1)
在△ADC中，因为EF∥CD，所以AD/AF=AC/AE（2）
由（1）（2）式得AB/AD=AD/AF，所以AD=AB.AF
即AD是AB和AF的比例中项。
例3 用平行于三角形且和其他两边相交的直线截三角形，所截得的三角形的三边与原角形的三边对应成比例。
已知，如图1-14，DE∥BC，DE分别交AB、AC于D、E，求证：AD/AB=AE/AC=DE/BC。
分析，由平行线分线段成比例定理的推理可以得到AD/AB=AE/AC，为了用平行线分线段成比例定理证明AE/AC=DE/BC，须要构造一组平行线，使AE、AC、DE、BC成为由平行线截得的线段只要过点E作EF、AB交BC于点F，就可以达到上述目的。
证明过点E作EF∥AB，交BC于点F，
因为DE∥BC，EF∥AB，所以AD/AB=AE/AC，BF/BC=AE/AC，
且四边形DEFB为平行四边形，故DE=BF。
则AE/AC=DE/BC，因为AD/AC=AE/AC=DE/BC。
“平行线分线段成比例定理”是平面几何中的定理，一个自然的想去是：这个定理在空间中也成立吗？请你完成这个探究。
实际上，命题的推广可以有不同的方向，例如，在“平行线玢线段成比例定理”中，如果将平行线改为平行平面也可以探究相应命题是否成立，请你完成下列探究。