课程内容

《平行线等分线段定理》
在初中，我们已经在平面几何中讨论过平行的一些性质和判定的问题，例如，如果两条直线同时平行于第三条直线，那么这两条直线互相平行；同位角相等，两直线平行，内错角相等……下面我们继续研究平行线的性质。
研究平行线的性质，就是在已知一组直线平行条件下，探究可以推出哪些结论，例如，一组平行线被另一组平行的或非平行的直线，，所得到的图形具有哪些性质？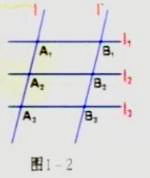
观察如图1-2三条直线l1、l2、l2满足l1∥l2,直线l2∥l3且分别与l1、l2、l3相交于A1、A2、A3和B1、B2、B2当A1A2=A2A3时，观察图形，长测线段B1B2、B2B3的长度，它们有什么关系？如果l与l不平行上述关系还成立吗？
已知l1∥l2∥l3,直线l、l1与l1、l1、l2分别将于A1、A2、A3和B1、B2、B3，如果A1A2=A2A3,那么B1B2=B2B3
证明（1）如图1-2，当l∥l时∵l1∥l2∥l3
∴四边形A1B2B3A2是平行四边形，
∵A1A2= B1B2
同理可证A2A3= B2B3
∵A1A2=A2A3∴B1B2=B2B3
（2）当l与l1不平行时，如图1-4，过B1作B1C2∥A1A2，交l于C2过B2作B2C2//A2A3，交L于C同（1）的证明方法可得BC=BC，考察△BCB和△BCB
∵B2C2∥B3C3（为什么？），∴∠C1B1B2=∠C2B2B3
又∵∠B1B2C1=∠B2B3C2，B2C1=B3C2,
∴△BCB≌△BCB,∴B1B2=B2B3于是，我们有
平行线等分线段定理，如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等。
将图1-4中的直线L1平移，使L1与L相交于A（图1-5），考察△A1A2B2，因为A1A2=A2A3，所以根据平行线等分线段定理可得AB=BB

于是有
推论1 经过三角形一边的中点与另一边平行的直线必平分第三边。
探究，考察图1-4中的梯形A2A3B3B2，你能发现什么结论？
推理2 经过梯形一腰的中点且与底边平行的直线必平分另一腰。
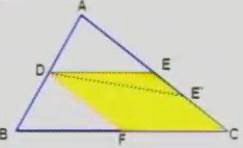
例1 如图1-7，D、E分别是△ABC中AB边和AC边的中点求证：DE∥BC且DE=1/2BC
这是我们尝过的三角形中位线定理下面我们用平行线等分线段定理证明它。
证明过D作DE∥BC，根据推理1，E1为AC的中点，故E与E1重合，即DE∥BC，两样，过D作DF∥AC，交BC于F，则BF=FC
∵DE∥FC，DE∥EC，
∴四边形DECE是平行四边形，
∴DE=FC，
又因为FC=1/2BC，所以DE=1/2BC
一个数学命题的发现往往来自于对特例的观察和概括，因为在特例中，其命题的各种信息会更加明显，容易被人们捕捉，从而更容易发现条件与结论的内在联系，将问题特殊化，通过特殊现象而得出一般的猜想或者通过解决特例而获得解决一般问题的思想方法的启示，这是数学研究中常用的方法请同学回顾平行线等分线段定理的概括过程，从中体会从特殊到一般的思想方法。