课程内容

《函数概念复习》

知识回顾
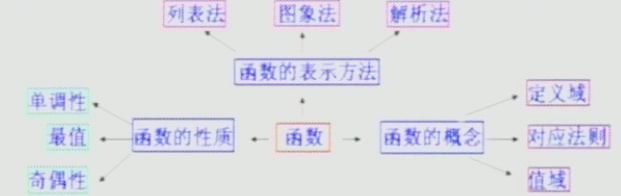
1.函数的基本概念
（1）函数定义
设集合A是一个非空的数集，如果按照某种确定的对应关系f，使对于集合A中任意一个数x，在集合B中都的唯一确定的数f（x）和它对应，那么就称f:A àB为从集合A到集合B的一个函数，记作y=f（x）,x∈A。
（2）函数的定义域、值域
在函数V=f（x）,x∈A中，x叫做自变量，x的取值范围A叫做函数的定义域；与x的值相对应的y值叫做函数值，函数值的集合｛f（x）∣x∈A｝叫做函数的值域，显然，值域是集合B的子集。
（3）函数的三要素：定义域、值域和对应法则。
（4）相等函数：如果两个函数的定义域相同，并且对应关系完全一致，则这两个函数相等，这是判断两个函数相等的依据。
2.函数的表示法
表示函数的常用方法：解析法、图象法和列表法。
3.映射的概念
设A，B是两个非空的集合，如果按照某一个确定的对应关系f，使对于集合A有任意一个元素x，在集合B中都有唯一确定的元素y与之对应，则称对应f：AàB是集合A到集合B的一个映射。
4.由映射的定义可以看出，映射是函数概念的推广，函数是一种特殊的映射，要注意构成函数的两个集合A，B必须是非空数集。
二、函数的性质
1.函数的单调性与最值
（1）单调性：对于定义域内某一个区间D内任意的x₁,x₂,且x₁＜x₂（或△x=x₁-x₂＜0）,
①若f（x₁）＜（x₂）（或△y=f（x₁）-f（x₂）＜0）恒成立f（x）在D上单调增；
②若f（x₁）﹥（x₂）（或△y=f（x₁）-f（x₂）﹥0）恒成立f（x）在D上单调减。
（2）最值：设函数y=f（x）的定义域为I，
①如果存在实数M满足；对任意的ｘ∈I，都有ｆ（x）≤Ｍ且存在ｘ∈R，使得ｆ（x）＝Ｍ，那么称M是函数y=f（x）的最大值；
②如果存在实数M满足；对任意x∈I，都有f（x）≥M且存在x∈R，使得f（x）=M,那么称M是函数y=f（x）的最小值。
2.函数的奇偶性
（1）定义：对于定义域内的任意x，有
①f（-x）=-f（x）<=>f（x）为奇函数；
②f（-x）=f（x）<=>f（x）为偶函数；
（2）性质
①函数y=f（x）是偶函数<=>y=f（x）的图象关于y轴对称。
函数y=f（x）是奇函数<=>y=f（x）的图象关于原点对称。
②奇函数在其定义域内关于原点对称的两个区间上的单调性相同，且在x=0处有定义时必有f（0）=0，即f（x）的图象过原点。
③偶函数在其定义域内适于原点对称的两个区间的单调性相反。
例题讲解
一、函数的概念
1.下列说法中，不正确的是（B）
A.函数值域中每一个数都有定义域中的至少一个数与之对应。
B.函数的定义域和值域一定是无限集合。
C.定义域和对应关系确定后，函数的值域也就确定了。
D.若函数的定义域只有一个元素，则值域也只有一个元素。 
二、函数图象的应用
例、设函数f（x）=x²-2∣x∣-1（-3≤x≤3）,
（1）证明f（x）是偶函数；（2）画出这个函数的图象；
（3）指出函数f（x）的单调区间，并说明在各个单调区间上f（x）是增函数还是减函数；
（4）求函数的值域。
1.设函数f（x）=x²-2∣x∣-1（-3≤x≤3）,
（1）证明f（x）是偶数；
（1）证明：定义域关于原点对称。
∵f（-x）=（-x）2-∣-x∣-1
         =x2-2∣x∣-1=f（x）
     即f（-x）=f（x）
     ∴f（x）是偶函数。
f（x）=x2-2∣x∣-1（-3≤x≤3）
（2）画出这个函数的图象
（2）当x≥0时，
f（x）=x²-2x-1=（x-1）²-2,
当x＜0时，f（x）=x²+2x-1=(x+1)²-2,
即f（x）=（x-1）²-2   （0≤x≤3）
         （x+1）²-2   （-3≤x≤0）
根据二次函数的作图方法，可得函数图象如图。
三、函数奇偶性和单调性的应用
1判断函数f（x）=√1-x²/∣x+2∣-2的奇偶性。
解：1-x2≥0       -1≦x≦1          -1≦x≦1且x≠0
    ∣x+2∣≠2    x≠0且x≠-4
∴定义域为[-1.0） υ （0.1]
∴f（x）=（√1-x2）/（x+2）-2=（√1-x²）/x
∵f（-x）=（√1-（-x）²）/-x=-（（√1-x²）/x）
即f（-x）=-f（x）  ∴f（x）为奇函数。