课程内容：

《探索勾股定理（二）》

知识回顾;

1.勾股定理的内容是什么？

2.它反映的是直角三角形中的那些基本量之间的关系？

3，我们是用什么方法得到这个结论的？

如果三角形中两边的平方和等于第三边的平方，那么这个三角形是直角三角形。

即如果三角形的三边长a,b,c有关系

        a²+b²=c²

那么这个三角形是直角三角形。

1 想一想：上述哪条边所对的角是直角？

2 这个定理可判断三角形是否是直角三角形

3 能够成为直角三角形三边长的三个正整数，称为勾股数（或勾股弦数）。

例1.根据下列条件，分别判断以a,b,c为边的三角形是不是直角三角形。

（1）a=7,b=24,c=25.

（2）a=2/3,b=1,c=2/3

课堂练习：

下列几组数能否作为直角三角形的三边长？说说你的理由。

（1）29,21,20

（2）5,7,8

（3）12,35,36

例2：已知△ABC的三边长分别为a,b,c,且a=m²-n²，b=2mn,c=m²+n².(m,n是正整数，且m＞n),△ABC是直角三角形吗?请说明理由。

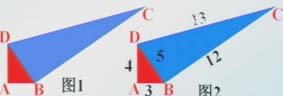
例3：一个零件的形状如图1所示，按规定这个零件中∠A和∠DBC都应为直角。个人师傅量得这个零件各边尺寸如图2所示，这个零件符合要求吗？

思考题：

1、四边形ABCD中已知AB=3，BC=4,CD=12，DA=13，且∠ABC=90°，求这个四边形的面积。

2、请你写出三组勾股数；

3、一组勾股数的倍数一定是勾股数吗？为什么？

4、四边形ABCD中，∠ACB=90°，AB=13，BC=5，AD=9，CD=15，回答下列问题

（1）AC的长是多少？

（2）△ABC，△ACD是直角三角形吗？为什么?

（3）这个四边形的面积是多少？