课程内容：

《直角三角形（二）》

直角三角形的性质2：

直角三角形斜边上的中线等于斜边的一半

数学语言表述为：

在Rt△ABC中
∵CD是斜边AB上的中线
∴CD=AD=BD=1/2AB

练一练：

1、已知Rt△ABC中，斜边AB=10cm,则斜边上的中线的长为________

2、在Rt△ABC中，CD是斜边AB上的中线，∠CDA=80°，则∠A=_____∠B=______

例1：如图，已知AD⊥BD，AC⊥BC，E为AB的中点，试判断DE与CE是否相等，并说明理由。

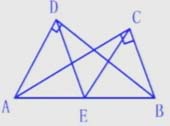
变式题：已知AD。BE分别是△ABC的BC、AC边上的高，F是DE的中点，G是AB的中点，则FG⊥DE，请说明理由。

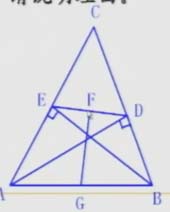
思考：

在Rt△ABC中，BD是斜边AC上的中线，∠A=30°
（1）∠C=_____∠ABD=____
∠BDC=______∠CBD=_____
（2）△BDC是什么三角形？
（3）此时BC与AC有什么关系？

直角三角形的性质3：

在直角三角形中，30°角所对的直角边等于斜边的一半。

练一练：

1 在Rt△ABC中∠A=30°，AB+BC=12cm,则AB=_______cm

2 △ABC是等边三角形，D,E分别在BC和AC上，AD⊥BC，DE⊥AB,若AB=8cm,BD=____,BE=_____

3 一名滑雪运动员沿着斜角为30°的斜坡，从A滑行至B。已知AB=200m,问这名滑雪运动员的高度下降了多少m?

4 在△ABC中，AB=AC=2a,∠ABC=∠ACB=15°，CD是腰AB上的高，求CD的长。