课程内容

《等可能事件的概率》（2）
学习目标
1、在具体情境中进一步理解概率的意义。
2、熟练进行概率的简单计算。
3、设计符合要求的概率模型。
复习：
1、摸到红球的概率？
   P（摸到红球）=摸出红球可能出现的结果数/摸出一球所有可能的结果数
2、三种事件发生的概率及表示？
①必然事件发生的概率为1，记作P（必然事件）=1；
②不可能事件发生的概率为0，记作P（不可能事件）=0；
③若A为不确定事件，则0＜P(A)＜1。
具体情境：
下图是卧室和书房地板的示意图，图中每一块方砖除颜色外完全相同，小猫分别在卧室和书房中自由地走来走去，并随意停留在某块方砖上。在哪个房间里，小猫停留在黑砖上的概率大？

议一议
假如小猫在如图所示的地板上自由地走来走去，并随意停留在某块方砖上，它最终停留在黑色方砖上的概率是多少？（图中每一块方砖除颜色外完全相同）

提示：概率大小与_________有关
想一想
（1）若条件不变，小猫最终停留在白色方砖上的概率是多少？
（2）这个概率等于“袋中装有12个黑球和4个白球，这些球除颜色外都相同，从中任意摸出一球是黑球”的概率吗？你是怎样想的？
例题
某商场为了吸引顾客，设立了一个可以自由转动的转盘，并规定：顾客消费100元以上，就能获得一次转动转盘的机会。如果转盘停止后，指针正好对准红、黄或绿色区域，顾客就可以分别获得100元、50元、20元的购物券（转盘被等分成20个扇形）。
1、甲顾客消费80元，是否可获得转动转盘的机会？
2，乙顾客消费120元，他获得购物券的概率是多少？他得到100元，50元，20元购物券的概率分别是多少？
分析：
乙顾客的消费额超过100元而不到200元，因此可以获得一次转动转盘的机会。
转盘被等分成20个扇形，其中1个是红色，2个是黄色，4个是绿色，对乙顾客来说：
解：P（获得购物券）=(1+2+4)/20=7/20
    P（获得100元购物券）=1/20
    P（获得50元购物券）=2/20=1/10
    P（获得20元购物券）=4/20=1/5
思维训练：
1、一位汽车司机准备去商场购物，然后他随意把汽车停在某个停车场内，停车场分A、B两区，停车场内一个停车位置正好占一个方格且一个方格除颜色外完全样，则汽车停在A区蓝色区域的概率是（   ），B区蓝色区域的概率是（   ）。

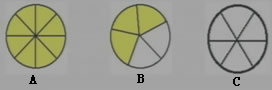
2、如图A、B、C三个可以自由转动的转盘，转盘被等分成若干个扇形，转动转盘，指针停止后，指向白色区域的概率分别是（   ）、（   ）、（   ）。

动手操作，设计模型
1、如图所示，转盘被分成8个相等的扇形，请在转盘的适当地方涂上颜色，使得自由转动这个转盘，当它停止转动时，指针落在绿色区域的概率为3/8。
2、如图所示：转盘被等分成16个扇形，请在转盘的适当地方涂上颜色，使得自由转动这个转盘，当它停止转动时，指针落在红色区域的概率为3/8。
3、小猫在如图所示的地板上自由地走来走去，它最终停留在红色方砖上的概率是1/4，你试着把每块砖的颜色涂上。
探索实践
一张写有密码的纸片被随意地埋在下图中的某个方块的下面（每个方格大小一样）。
（1）埋在哪个区域的可能性大？
（2）分别计算埋在三个区域的概率。
（3）埋在哪两个区域的概率相同？
试一试
从甲地到丙地需经过乙地。从甲地到乙地有3条路线A1、A2、A3，从乙地到丙地有2条路线B1、B2，其中A3B2最短路线。某人任选了一条从甲地到丙地的路线，它正好是最短路线的概率是多少？
归纳总结
1、有时概率的计算和面积有关。
2、设计符合条件的概率模型。