课程内容
《平行线的性质》
温故知新
判定两条直线平行,我们学过的方法有哪些?
一、定义:同一平面内,两直线无公共交点。
二、同位角、内错角相等或同旁内角互补可以判断两条线平行。
心灵手巧画一画:
借助练习本上的横线格,画两条平行线被第三条直线所截。
探索新知
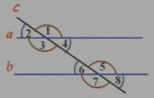
如图:直线a与直线b平行
(1)图中有几对同位角,请分别找出来。
(2)任选其中的一对同位角,用量角器量出它们的度数,并比较它们的大小。
(3)其他同位角的大小也有这种关系吗?
(4)由此你可得到什么结论?
两条平行线被第三条直线所截,同位角相等。
简记:两直线平行,同位角相等。
类似地,你能得到两条直线平行时,内错角之间的关系吗?
两直线平行,内错角相等。
类似地,你能得到两条直线平行时,同旁内角呢?
两直线平行,同旁内角互补。
学习重点:平行线的性质
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
基础练习
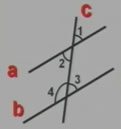
1、如图,直线a∥b,∠1=54°,则∠2=_____,根据是_______;∠3=_____,根据是_______;∠4=_____,根据是_______。
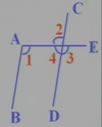
2、如图,已知直线AB∥CD且被AE所截。
(1)∠1=110°,则∠2=_____。( )
(2)∠1=110°,则∠3=_____。( )
(3)∠1=110°,则∠4=_____。( )
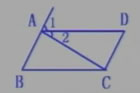
3、如图,已知AB∥CD,AD∥BC,填空:
(1)∵AB∥CD(已知)
∴∠1=______(两直线平行,内错角相等。)
(2)∵AD∥BC(已知)
∴∠2=______( )
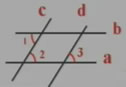
4、如图:已知直线a∥b,直线c∥d,∠1=70°,则∠2的度数=____,根据是___________,∠3的度数=____,根据是___________。
实际应用 优势互补
如图是举世闻名的三星堆考古中发掘出的一个残缺玉片,通过整理发现这是一块梯形玉片,量得∠A=115°,∠D=100°。请你求出另外两个角的度数。
生活中的数学
如图,当两个人的目光相对时,视线与水平线所成的角相等吗?为什么?
议一议:
平行线的判定和性质有什么共同点和不同。
| 性质 | 判定 | ||
| 由“线”(平行)知“角”(相等或互补) | 由“角”(相等或互补)定“线”(平行) | ||
| 两直线平行 | 同位角相等 | 同位角相等 | 两直线平行 |
| 内错角相等 | 内错角相等 | 两直线平行 | |
| 同旁内角互补 | 同旁内角互补 | 两直线平行 | |
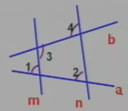
已知:如图,已知∠1=∠2,∠3=115°。求∠4的度数。
突破难点
如图,一束平行光线AB和DE射向一个水平镜面后被反射。
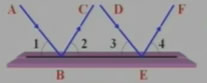
(1)∠1,∠3的大小有什么关系?
(2)反射光线BC与EF也平行吗?
挑战自我
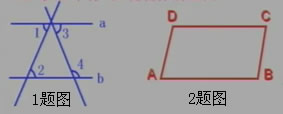
1、如图,已知∠1=∠2,∠3=65°。求∠4的度数。
2、如图,已知AD∥BC,∠A=∠C,AB与CD平行吗?说说你的理由。
感悟反思
本节课学习了平行线的性质,总结了平行线的判定与性质的区别。
条件:角的关系→平行关系
特征:平行关系→角的关系




























