课程内容

《应用二元一次方程组——里程碑上的数》
学习目标
1、掌握用二元一次方程组解决“里程碑上的数”这一有趣场景中的数字问题。
2、进一步经历和体验列方程组解决实际问题的过程，体会方程（组）是刻画现实世界的有效数学模型，熟练掌握列方程组解决实际问题的一般方法与步骤。
填空。
1、如果一个两位数的十位数字为x，个位上的数字为y，那么这个两位数可表示为_________；如果交换个位和十位数字，得到的新两位数为_________。
2、两个两位数分别为x和y，如果将x放到y的右边就得到一个四位数，那么这个四位数可表示为_________；如果将x放到y的左边就得到—个新的四位数，那么这个新的四位数可表示为_________。
3、一个两位数的十位数字为x，个位上的数字为y，如果在它们的中间加一个零，变成一个三位数，那么这个三位数可表示为_________。
数字问题：
一、小明的爸爸骑摩托车带着小明在公路上匀速行驶，下面是小明每隔1小时看到的里程情况。你能确定小明在12:00时看到的里程上的数么？
12:00：是一个两位数，它的两个数字之和为7。
13:00：十位数字和个位数字与12:00所看到的正好互换了。
14:00：比12:00所看到的两位数中间多了个0。
解：设小明在12:00时看到的数的十位数字是x，个位数字时y，根据题意，得
 
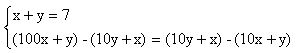
  解得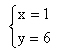
答：小明在12:00看到的数是16。
二、两个两位数的和是68，在较大两位数的右边接着写较少的两位数，得到一个四位数；在较大两位数的左边接着写较少的两位数，也得到一个四位数；已知前一个四位数比后一个四位数大2178，求这两个两位数。
分析：设较大的两位数为x，较少的两位数为y，则前一个四位数为多少？后一个四位数又是多少？
  100x+y     100y+x
随堂练习
1、已知一个两位数，减去它的各位数字之和的3倍，结果是23；这个两位数除以它的各位数字之和，商是5，余数是1。求这个两位数。
2、小明和小亮做加法游戏，小明在一个加数的后面多写一个0，所得和是242；而小亮在另一个加数的后面少写一个0，所得到的和是341。求原来的两个加数。
小结与收获
1、经过本节课的学习，你有哪些收获？
2、列二元一次方程组解实际问题的一般步骤：
（1）审题；
（2）设两个未知数，找两个等量关系；
（3）根据等量关系列方程，联立方程组；
（4）解方程组；
（5）检验并作答。