课程内容

《应用二元一次方程组——鸡兔同笼》
学习目标
1、使学生初步掌握列二元一次方程组解应用题的方法与步骤。
2、通过将实际问题转化成纯数学问题的应用训练，培养学生分析问题、解决问题的能力。
3、通过对祖国文明史的了解，培养学生爱国主义精神，树立为中华崛起而学习的信心。
鸡兔同笼
今有鸡兔同笼，
上有三十五头，
下右九十四足，
问鸡兔各几何？
“鸡兔同笼”是一类有名的中国古算题，最早见于《孙子算经》下卷第31题“雉兔同笼”，流传广泛，许许多多数学应用题都可以转化成这类问题来解决，或者用解决“鸡兔同笼”问题的解法来解决。
“雉兔同笼”题：今有雉（鸡）兔同笼，上有35头，下有94足，问雉兔各几何？
（1）《孙子算经》中记载的算法：
     金鸡独立，兔子站起
     数脚：94÷2=47（只）
     头数：兔 47-35=12（只）
           鸡 35-12=23（只）
总脚数÷2-总头数=兔子数
能够这样算，主要是利用了兔和鸡的脚数分别是4和2，4又是2的倍数。可是当其他问题转化成这类问题时，数就不一定是4和2，上面的计算方法就行不通。
1、“上有35头”的意思是什么？“下有94足”呢？
2、你能根据（1）中的数量关系列出方程吗？
3、你能解决这个有趣的问题吗？
解：设笼中有鸡x只，有兔y只，由题意可得：
   
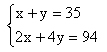
    解此方程组得：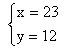
答：笼中有鸡23只，兔12只。
例1：以绳测井。若将绳三折测之，绳多五尺；若将绳四折测之，绳多一尺。绳长、井深各几何？
题目大意：用绳子测水井深度，如果将绳子折成三等份，一份绳长比井深多5米；如果将绳子折成四等份，一份绳长比井深多1尺。问绳长、井深各是多少尺？
等量关系：
  （井深+5）×3=绳长
  （井深+1）×4=绳长
解：设绳长x尺，井深y尺，则由题意得
   
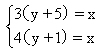
    解此方程组得：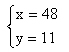
所以绳长48尺，井深11尺。
练习
1、设甲数为x，乙数为y，则甲数的2倍与乙数的3倍的和为15，列出方程为__________。
2、一只蛐蛐6条腿，一只蜘蛛8条腿，现有蛐蛐和蜘蛛共10只，共有68条腿，若设蛐蛐有x只，蜘蛛有y只，则列出方程组__________。
3、小刚有5角硬币和一元硬币有8枚，币值共有6元5角，设5角的有x枚，一元的有y枚，列出的方程组为__________。
4、甲、乙两人参加植树活动，两人共植树20棵，已知甲植树数是乙的1.5倍。如果设甲植树x棵，乙植树y棵，那么可列方程组为（   ）

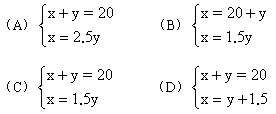
5、做一做：
列方程组解古算题：
“今有牛五、羊二，直金十两。牛二、羊五，直金八两。牛、羊各直金几何？”
题目大意是：5头牛、2只羊共价值10两“金”。2头牛、5只羊共价值8两“金”。每头牛、每只羊各价值多少“金”？
6、买一些4分和8分的邮票，共花6元8角，已知8分的邮票比4分的邮票多40张，那么两种邮票各买了多少张？