课程内容
《用二元一次方程组确定一次函数表达式》
回顾与思考
1、判断下列函数关系式中的y是不是x的一次函数。
(1)y=-x (2)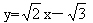
(3)y=3(x-1) (4)y-x=2
(5)y=x3 (6)y=1/x
2、函数y=-4x+3中,y的值随x的增大而_________
3、有同学画了如图所示的一条直线,你能知道他画的直线的表达式是什么?
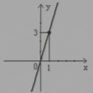
想一想
1、正比例函数y=kx图象的特点。
2、一次函数y=kx+b的图象是什么图形?
3、在y=3x+b,y=kx+2,y=3x+2中哪一个函数的图象可以确定下来?为什么?
试一试
某物体沿一个斜坡下滑,它的速度(米/秒)与其下滑时间t(秒)的关系如右图所示:

(1)请写出v与t的关系式;
(2)下滑3秒时物体的速度是多少?
想一想
确定正比例函数的表达式,就是要确定哪个值?k(自变量的系数)
需要(原点除外)几个点坐标呢?一次函数呢?k、b的值
总结:在确定函数表达式时,要求几个系数就需要知道几个点的坐标。
例1 在弹性限度内,弹簧的长度y(厘米)是所挂物体质量x(千克)的一次函数。一根弹簧不挂物体时长14.5厘米;当所挂物体的质量为3千克时,弹簧长16厘米。请写出y与x之间的关系式,并求当所挂物体的质量为4千克时弹簧的长度。
思考:确定一次函数表达式所需要的步骤是什么?
1、设——设函数表达式y=kx+b
2、代——将点的坐标代入y=kx+b中,列出关于k、b的方程
3、求——解方程,求k、b
4、写——把求出的k、b值代回到表达式中即可
解:设y=kx+b(k≠0)
由题意得:14.5=b,
16=3k+b,
解得:b=14.5 k=0.5
所以在弹性限度内,y=0.5x+14.5
当x=4时,y=0.5×4+14.5=16.5(厘米)
即物体的质量为4千克时,弹簧长度为16.5厘米。
已知函数图象确定函数表达式
如图所示,已知直线AB和x轴交于点B,和y轴交于点A。
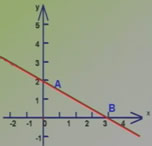
①写出AB两点的坐标。
②求直线AB的表达式。
学以致用
①若一次函数图象y=2x+b经过点(-1,1),则b=_____,该函数图象经过点B(1,___)和点C(___,0)。
②如图,直线l是一次函数y=kx+b的图象,
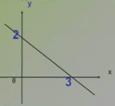
(1)b=( ),k=( )
(2)当x=30时,y=( )
(3)当y=30时,x=( )
(4)你能求出三角形AOB的面积吗?
补充:利用表格信息确定函数表达式
某汽车对其A型汽车进行耗油实验,y(耗油量)是t(时间)的一次函数,函数关系如下表,请确定函数表达式。
| t(时间) | 0 | 1 | 2 | 3 | … |
| y(耗油量) | 100 | 84 | 68 | 52 | … |
④根据条件确定一次函数表达式:y是x的正比例函数,当x=2时,y=6,求y与x的函数表达式。
⑤若函数y=kx+b的图象经过点(0,5)(1,6),求k,b及表达式。
胜利的彼岸
①若一次函数图象y=ax+3的图象经过A(1,-2),则a=( )
②直线y=2x+b过点(1,-2),则它与y轴交点坐标为( )
③某函数具有下列两条性质:它的图象经过原点(0,0)的一条直线;y值随x的增大而减小。
请你写出满足上述条件的函数(用关系式表示)
你能行
某地长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定,则需要购买行李票,行李票费用y元是行李质量x(千克)的一次函数,其图象如下图所示:
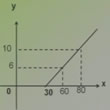
①写出y与x之间的函数关系式;
②旅客最多可免费携带多少千克行李?
总结
确定正比例与一次函数表达式的条件。
由于正比例y=kx(k≠O)中,只有一待定系数K,所以只要一个条件(如一组对应的值),就可以求出k的值。
一次函数y=kx+b有两个待定系数k、b,需要两个独立的条件确定关于的方程,求得的值,这两个条件通常是两组对应的x、y值。
确定一次函数表达式的方法。




























