课程内容

《认识三角形》
自学阅读
阅读课本P63，第2、3、4、5段内容，并回答以下问题：
（1）什么叫三角形？
（2）三角形有几条边？有几个内角？有几个顶点？
（3）三角形ABC用符号表示_________。
（4）三角形ABC的边AB、AC和BC可用小写字母分别表示为_________。
1、三角形的定义
   由不在同一条直线上的三条线段首尾顺次相接所组成的图形，叫做三角形。
2、三角形的相关概念
（1）三角形的边：AB、BC、CA
     三角形中组成这个三角形的三条线段，就叫三角形的边。
（2）三角形的内角：∠A、∠B、∠C
     相邻两边所组成的角叫做三角形的内角。
（3）三角形的顶点：点A、点B、点C
    相邻两边的公共端点叫做三角形的顶点。
温馨提示：
  顶点A所对的边是_____，还可用“___”表示；
  顶点B所对的边是_____，还可用“___”表示；
  顶点C所对的边是_____，还可用“___”表示。
3、三角形的表示方法：
三角形用符号“△”表示，记作“△ABC”，读作“三角形ABC”。
温馨提示：表示三角形时，字母没有先后顺序。
慧眼识别：
（1）图中有几个三角形？分别用符号表示这些三角形。

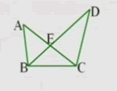
（2）以AB为边的三角形有哪些？
（3）以E为顶点的三角形有哪些？
（4）以∠D为角的三角形有哪些？
（5）说出△BCD的三个角和三个顶点所对的边。
4、三角形的分类
（1）按角分类：锐角三角形、直角三角形、钝角三角形
（2）按边分类：不等边三角形、等腰三角形
在等腰三角形中，相等的两边都叫做腰，另一边叫做底，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。
等腰三角形可以分为：
（1）底边和腰不相等的等腰三角形
（2）等边三角形
5、三角形三边之间的关系
探究：画一个任意△ABC，假设有一只小虫要从点B出发沿着三角形的边爬到点C，它有几条线路可以选择？各条路线的长一样吗？
结论：三角形三边之间的关系：三角形任意两边的和大于第三边。
知识应用
下列长度的三条线段能否组成三角形？为什么？
（1）3，4，8     （2）5，6，11     （3）5，6，10
思考：判断三条线段能否组成三角形，是否一定要检验三条线段中任何两条的和都大于第三条？根据你以上解题经验，有没有更简便的判断方法？
  判断技巧：比较较小的两边之和与最长边的大小。
例题选讲
用一根长为18厘米的细铁丝围成一个等腰三角形。
（1）如果腰长是底边的2倍，那么各边的长是多少？
（2）能围成有一边的长为4厘米的等腰三角形吗？为什么？
学以致用
1、已知等腰三角形的一边等于7，一边等于8，求它的周长。
2、已知等腰三角形的一边等于6，一边等于13，求它的周长。