课程内容

《基本不等式√ab≤(a+b)/2（1）》
经“风车”抽象成左图。在正方形ABCD中有4个全等的直角三角形。令直角三角形两条直角边的长为a、b。
S_△DGC=1/2ab，即4个直角三角形的面积和为2ab，正方形的面积为a²+b²。
由此得：一般地，对于任意实数a、b，我们有a²+b²≥2ab，当且仅当a=b时，等号成立。
一、不等式（1）a²+b²≥2ab
还有其他的方法证明吗？
如果a＞0，b＞0，我们用√a，√b分别代替a、b，可得a+b≥2√ab
通常我们把上式写作：√ab≤（a+b）/2（a＞0，b＞0）
二、基本不等式或不等式（2）
√ab≤（a+b）/2（a＞0，b＞0）或者（a+b）/2≥√ab（a＞0，b＞0）
当且仅当a=b时，（a+b）/2=√ab
1、两个正数的算术平均数大于或等于它们的几何平均数。
2、两个正数的等差中项大于或等于它们正的等比中项。
探究：如何证明基本不等式√ab≤（a+b）/2（a＞0，b＞0）？
探究：法2与法3的证明有何不同？如何来使用？
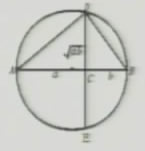
在右图中，AB是圆的直径，点C是AB上的一点，AC=a，BC=b，过点C作垂直于AB的弦DE，连接AD、BD，你能利用这个图形得出基本不等式√ab≤（a+b）/2是几何解释吗？

三、变形不等式与等价关系式
a、变形不等式
已知a，b为正数，证明下列结论

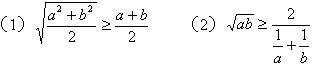
b、3个等价关系式
（1）a²+b²≥2ab ←→ ab≤（a²+b²）/2  （a，b∈R）
（2）√ab≤（a+b）/2 ←→ ab≤[（a+b）/2]²  （a，b∈R⁺）
（3）√[(a²+b²)/2]≥（a+b）/2 ←→ （a+b）²/2  （a，b∈R⁺）
其中当且仅当a=b时取等号。
四、基本不等式的简单应用
例1：证明下列两个不等式
（1）当a，b∈R+时，a/b+b/a≥2（当且仅当a=b时取“=”号）
（2）当a∈R⁺时，a+1/a≥2（当且仅当a=1时取“=”号）
例2：已知x，y是正数，求证：
（1）如果积xy是定值p，那么当且仅当x=y时，和x+y有最小值2√p。
（2）如果和x+y是定值s，那么当且仅当x=y时，积xy有最大值（1/4）s²。
课堂思考
某金店有一不准确的天平（臂长不等），顾客要买一串金项链，店主分别把项链放于左右两盘各称一次，然后把两次称得质量的算术平均数作为项链的质量，问这种称法是否合理？