课程内容

《二元一次不等式（组）与平面区域》
一、举例引出定义
实例：一家银行的信贷部计划年初投入25000000元用于企业和个人贷款，希望这笔资金至少可带来30000元的收益，其中从企业贷款中获益12%，从个人贷款中获益10%，那么，信贷部应该如何分配资金呢？
有关定义：
（1）二元一次不等式：
含有两个未知数，并且未知数的最高次数是1的不等式叫做二元一次不等式。
（2）二元一次不等式组：
由几个二元一次不等式组成的不等式组称为二元一次不等式组。
（3）二元一次不等式（组）的解集：
满足二元一次不等式（组）的x和y的取值构成有序实数对（x，y），所有这样的有序实数对（x，y）构成的集合称为二元一次不等式（组）的解集。
二、二元一次不等式（组）的解集表示的图形
（1）回忆、思考
回忆：初中一元一次不等式（组）的解集所表示的图形
（2）二元一次不等式（组）的解集表示什么图形呢？
先研究具体的二元一次不等式x-y＜6的解集所表示的图形。
因此，在平面直角坐标系中，不等式x-y＜6表示直线x-y=6左上方的平面区域，类似的，二元一次不等式x-y＞6表示直线x-y=6右上方的平面区域。如图。
直线叫做这两个区域的边界（虚线表示区域不包括边界直线）。
通过这个例子推广到一般情况：
（3）结论：二元一次不等式Ax+By+C＞0或Ax+By+C＜0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。（虚线表示区域不包括边界）
三、二元一次不等式（组）表示平面区域的判定方法
方法（1）：取点法（常取坐标原点）
方法（2）：当B＞0时，Ax+By+C＞0表示的点在对应直线的上方（左上方或右上方），Ax+By+C＜0表示的点在对应直线的下方（左下方或右下方），B＜0则相反，B=0呢？
应该注意的几个问题：
1、应准确判断不等式表示的平面区域在对应直线的哪一侧
2、若不等式中不含0，则边界应画成虚线，否则应画成实线。
3、画图时应非常准确，否则将得不到正确结果。
4、不等式组表示的平面区域是各个不等式所表示的平面点集，因而是各个不等式所表示的平面区域的公共部分。
四、应用
例1：画出不等式2x+y-6＜0表示的平面区域。
例2：画出不等式组2x+y-2≤0表示的平面区域。
                x-y-2≥0
例3：画出不等式（x+2y+1）（2x+y-2）＜0表示的平面区域。
例4：画出不等式组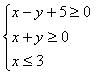表示的平面区域。
例5：一个化肥厂生产甲、乙两种混合肥料，生产1车皮甲种肥料的主要原料是磷酸盐4t，硝酸盐18t；生产1车皮乙种肥料需要的主要原料是磷酸盐1t，硝酸盐15t。现库存磷酸盐10t，硝酸盐66t，在此基础上生产这两种混合肥料。列出满足生产条件的数学关系式，并画出相应的平面区域。