课程内容

《不等关系与不等式（2）》
一、复习回顾
1、用不等式或不等式组表示不等关系
2、a＞b←→a-b＞0
   a=b←→a-b=0
   a＜b←→a-b＜0
3、比较两个数或代数式的大小——作差比较法
作差→变形→判断符号→得出结论
二、不等式的性质
性质1：如果a＞b，那么b＜a；如果b＜a，那么a＞b。
性质1表明：把不等式的左边和右边交换位置，所得不等式与原不等式异向，我们把这种性质称为不等式的对称性。
性质2：如果a＞b，b＞c，那么a＞c。
这个性质也可以表示为c＜b，b＜a，则c＜a。这个性质是不等式的传递性。
性质3：如果a＞b，则a+c＞b+c。
性质3表明，不等式的两边都加上同一个实数，所得的不等式与原不等式同向。
a+b＞c→a+b+（-b）＞c→a＞c-b
结论：不等式中的任何一项都可以改变符号后移到不等式另一边（移项法则）。
性质4：如果a＞b，c＞0，则ac＞bc；如果a＞b，c＜0，则ac＜bc。（可乘性）
性质5：如果a＞b，c＞d，则a+c＞b+d。（加法性质）
几个同向不等式的两边分别相加，所得的不等式与原不等式同向。
性质6：如果a＞b＞0，c＞d＞0，则ac＞bd。（乘法性质）
几个两边都是正数的同向不等式的两边分别相乘，所得的不等式与原不等式同向。
性质7：如果a＞b＞0，那么aⁿ＞bⁿ，（n∈N，n≥2）（乘方法则）
性质7说明，当不等式两边都是正数时，不等式两边同时乘方所得的不等式和原不等式同号。
性质8：如果a＞b＞0，那么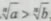，（n∈N，n≥2）
性质8说明，当不等式的两边都是正数时，不等式两边同时开方所得不等式与原不等式同向。
性质7、8可归纳为：a＞b＞0 ←→ aⁿ＞bⁿ，（n∈R，n＞0）
性质9：a＞b，ab＞0 → 1/a＜1/b（倒数法则）
以上这些关于不等式的事实和性质是解决不等式问题的基本依据。
三、应用
例1：对于实数a，b，c，判断下列命题的真假
（1）若a＞b则ac²＞bc²
（2）若ac2＞bc2则a＞b
（3）若a＜b＜0则1/a＜1/b
（4）若a＜b＜0则b/a＜a/b
（5）若a＜b＜0则a²＞ab＞b²
例2：已知a＞b＞0，c＜0，求证c/a＞c/b。
例3：应用不等式的性质，证明下列不等式。
已知a＞b＞0，0＜c＜d，求证a/c＞b/d。
例4：a＞b＞0，c＜d＜0，e＜0，则e/（a-c）＞e/（b-d）。
例5：（1）如果30＜x＜36，2＜y＜6，求x-2y及x/y的取值范围。
（2）若-3＜a＜b＜1，-2＜c＜-1，求（a-b）c2的取值范围。