课程内容

《正切函数的性质与图象》
复习：怎样利用单位圆中的正弦线作出y=sinx的图象？
思考：能否用正切线作正切函数图象呢？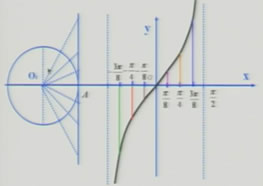

tan（x+π）=tanx，即：T=π。
思考：请同学观察正切函数的图象推出性质？
正切函数的性质
（1）定义域
     {x|x≠π/2+kπ，k∈Z}
（2）值域
     全体实数R
（3）周期性
∵tan（x+π）=tanx
正切函数是周期函数，T=π
（4）奇偶性
∵tan（-x）=-tanx
正切函数是奇偶性，正切曲线关于原点对称
正切函数的对称中心（kπ/2,0）k∈Z
（5）单调性
正切函数在开区间（-π/2+kπ，π/2+kπ），k∈Z内都是增函数。
强调：
a、不能说正切函数的整个定义域内是增函数；
b、正切函数在每个单调区间内都是增函数；
c、每个单调区间都跨两个象限：四、一或二、三。
例1：求函数y=tan（πx/2+π/3）的定义域、周期和单调区间。
例2：观察正切曲线写出满足下列条件的x的值的范围：tanx>0。
例3：不通过求值，比较tan135°与tan138°的大小。
补充练习
1、若函数y=-tan（πx/a-π/3）的最小正周期为2，则a=______。
2、函数y=2tan（π/3-x/2）的定义域为______；值域______；周期性______。
3、函数y=tan（2x+π/3）的图象是将tan2x的图象向______平移______个单位而得到的。