课程内容

《正弦函数、余弦函数的图象》
复习：
1、sinα，cosα，tanα的几何意义是什么？
2、如何用描点法作出函数y=x2-2x的图象？
3、等否用描点法作函数y=sinx，x∈[0,2π]的图象？
4、等否不通过查表得到点（x，sinx）的坐标？
新课讲解：
1、函数y=sinx，x∈[0,2π]图象的几何作法：
既然作与单位圆有关的三角函数线可得相应的角的三角函数值，那么通过描点（x，sinx），连线即可得到函数y=sinx，x∈[0,2π]的图象。
2、函数y=sinx，x∈R的图象：
因为终边相同的角有相同的三角函数值，所以函数y=sinx，x∈[2kπ,2（k+1）π]，k∈Z且k≠0的图象，与函数y=sinx，x∈[0,2π]的图象形状完全相同，只是位置不同，只要通过平移y=sinx，x∈[0,2π]的图象就可以得到函数y=sinx，x∈R的图象。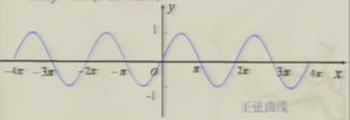

3、函数y=cosx，x∈R的图象：
由诱导公式y=cosx=sin（x+π/2）可以看出：余弦函数y=cosx，x∈R与函数y=sin（x+π/2），x∈R是同一个函数，余弦函数的图象可通过将正弦曲线向左平移π/2个单位长度而得到。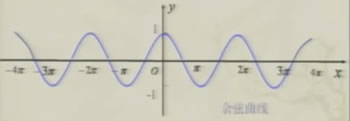

简图作法：
（1）列表（列出对图象形状起关键作用的五点坐标）
（2）描点（定出五个关键点）
（3）连线（用光滑的曲线顺次连结五个点）
例题讲解：
例：用“五点法”作出函数y=1+sinx，x∈[0,2π]的简图。
练：画出下列函数的简图。
（1）y=2sinx，x∈[0,2π]
（2）y=sin2x，x∈[0,2π]