课程内容：

《简单的三角恒等变换》
教学目标：
1.通过二倍角的变形公式推导半角的正弦、余弦、正切公式，体会划归、换元、方程、逆向使用公式等数学思想，提高推理能力。
2.理解并掌握二倍角的正弦、余弦、正切公式，并会利用公式进行简单的恒等变换，体会三角恒等变换在数学中的应用。
3.引导学生对变换对象进行对比、分析，促使学生形成对解题过程中如何选择公式，如何根据问题的条件进行公式变形，以及变换过程中体现的换元、逆向使用公式等数学思想方法的认识，提高推理能力。
教学重点：
    引导学生以已有的11个公式为依据，以推导积化和差、和差化积、半角公式作为基本训练，学习三角变换的内容、思路和方法。在与代数变换相比较中，体会三角变换的特点，提高推理、运算能力。
教学难点：
1.三角恒等变换及灵活运用。
2.灵活利用公式，通过三角恒等变换解决函数的最值、周期、单调性等问题。
3.灵活应用和、差、倍角公式的进行三角式化简、求值、证明。
思考：α与α/2有什么样的关系？
例1.试以cosα表示sin²α/2，cos²α/2，tan²α/2。
思考：代数式变换与三角变换有什么不同？
例2.已知sinα=5/13，且α在第二象限，求tanα/2的值。
例3.求证：
（1）sinαcosβ=1/2[sin（α+β）+sin（α-β）]
（2）sinθ+sinφ=2sin（θ+φ）/2cos（θ-φ）/2
例4.已知0＜α＜π/2，tanα=3/4，求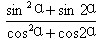的值。
例5.已知函数f（x）cos4x-2sinxcosx-sin4x。
（1）求f（x）的最小正周期；
（2）当x∈[0，π/2]求f（x）的最小值。