课程内容:
《平面向量数量积(2)》
教学目标:
1.掌握平面向量数量积及运算律;
2.能利用数量积的5个重要性质及数量积运算律解决有关问题;
3.掌握两个向量共线、垂直的几何判断,会证明两向量垂直,以及能解决一些简单问题。
教学重点:平面向量积及运算律。
教学难点:平面向量数量积的应用。
复习引入:
1.平面向量的数量积(内积)的定义:
已知两个非零向量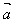 和
和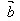 ,它们的夹角为θ,我们把数量│
,它们的夹角为θ,我们把数量│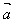 ││
││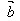 │cosθ叫做
│cosθ叫做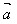 与
与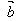 的数量积(或内积)。
的数量积(或内积)。
记为: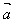 ·
·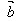 ,即
,即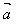 ·
·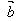 =│
=│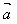 ││
││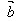 │cosθ
│cosθ
规定:零向量与任一向量的数量积为0,即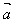 ·
·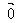 =0。
=0。
2.两个向量的数量积的性质:
设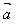 、
、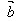 为两个非零向量,
为两个非零向量,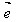 是与
是与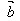 同向的单位向量。
同向的单位向量。
(1)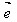 ·
·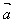 =
=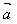 ·
·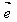 =│
=│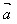 │cosθ
│cosθ
(2)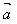 ⊥
⊥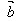 ←→
←→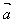 ·
·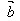 =0
=0
(3)当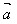 与
与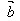 同向时,
同向时,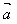 ·
·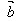 =│
=│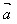 ││
││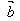 │
│
当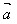 与
与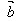 反向时,
反向时,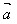 ·
·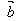 =-│
=-│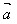 ││
││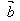 │
│
特别地,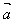 ·
·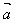 =│
=│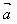 │2或│
│2或│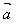 │=√
│=√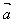 ·
·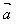
(4)cosθ=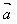 ·
·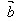 /│
/│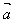 ││
││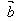 │
│
(5)│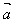 ·
·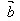 │≤│
│≤│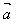 ││
││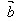 │
│
探究:
已知两个非零向量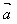 =(x1,y1),
=(x1,y1),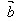 =(x2,y2)怎样用
=(x2,y2)怎样用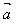 和
和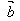 的坐标表示
的坐标表示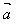 ,
,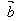 ?
?
1.平面两向量数量积的坐标表示:
两个向量的数量积等于它们对应坐标的乘积的和。
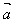 ·
·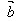 =x1x2+y1y2
=x1x2+y1y2
2.平面内两点间的距离公式:
(1)设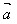 =(x,y),则│
=(x,y),则│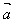 │2=x2+y2 或│
│2=x2+y2 或│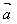 │=√x2+y2
│=√x2+y2
(2)如果表示向量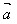 的有向线段的起点和终边的坐标分别为(x1,y1)、(x2,y2)那么:
的有向线段的起点和终边的坐标分别为(x1,y1)、(x2,y2)那么:
│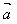 │=
│=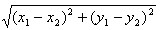 (平面内两点间的距离公式)
(平面内两点间的距离公式)
3.向量垂直的判定:
设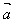 =(x1,y1),
=(x1,y1),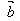 =(x2,y2)则
=(x2,y2)则 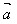 ⊥
⊥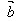 ←→x1x2·y1y2=0
←→x1x2·y1y2=0
4.两向量夹角的余弦:(0≤θ≤π)
cosθ=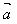 ·
·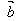 /│
/│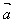 ││
││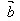 │=
│=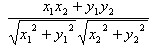
例1.已知A(1,2),B(2,3),C(-2,5),试判断△ABC的形状,并给出证明。
例2.在△ABC中,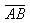 =(2,3),
=(2,3),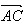 =(1,k),且△ABC的一个内角为直角,求k值。
=(1,k),且△ABC的一个内角为直角,求k值。
例3.已知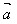 =(1,√3),
=(1,√3),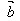 =(√3+1,√3-1),则
=(√3+1,√3-1),则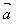 与
与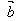 的夹角是多少?求与
的夹角是多少?求与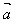 垂直的单位向量的坐标是多少?
垂直的单位向量的坐标是多少?
例4.已知A(3,2),B(-1,-1),若点P(x,-1/2)在线段AB的中垂线上,则x=____。