课程内容:
《平面向量数量积(1)》
教学目的:
1.掌握平面向量的数量积及其几何意义;
2.掌握平面向量数量积的重要性质及运算律;
3.了解用平面向量的数量积解决垂直的问题;
4.掌握向量垂直的条件。
教学重点:平面向量的数量和定义。
教学难点:
1.平面向量数量积的定义及运算律的理解;
2.平面向量数量积的应用。
复习:
1.两个非零向量夹角的概念:已知非零向量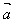 和
和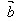 ,作
,作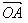 =
=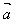 ,
,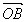 =
=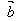 ,则∠AOB=θ(0≤θ≤π)叫做向量
,则∠AOB=θ(0≤θ≤π)叫做向量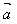 和
和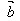 的夹角。
的夹角。
(1)θ=0时,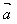 与
与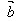 同向;
同向;
(2)θ=π时,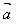 与
与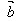 反向;
反向;
(3)θ=π/2时,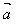 ⊥
⊥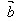 ;
;
(4)注意两向量的夹角定义,两向量必须是同起点的,范围是0≤θ≤π。
2.两向量共线的判定
设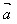 =(x1,y1),
=(x1,y1),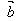 =(x2,y2),其中
=(x2,y2),其中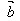 ≠0。
≠0。
3.我们都学过向量有关的哪些运算?
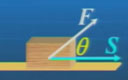
4.力做的功:
W=│F│·│s│cosθ,θ是F与s的夹角。
讲授新课:
1.平面向量的数量积(内积)的定义:
已知两个非零向量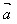 和
和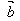 ,它们的夹角为θ,我们把数量│
,它们的夹角为θ,我们把数量│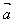 ││
││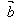 │cosθ叫做
│cosθ叫做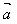 与
与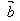 的数量积(或内积)。
的数量积(或内积)。
记为: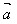 ·
·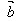 ,即
,即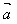 ·
·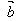 =│
=│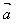 ││
││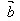 │cosθ
│cosθ
规定:零向量与任一向量的数量积为0,即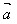 ·
·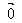 =0。
=0。
2.投影的概念:
│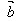 │cosθ叫做向量
│cosθ叫做向量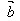 在
在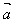 方向上的投影,投影也是一个数量,不是向量。
方向上的投影,投影也是一个数量,不是向量。
3.向量的数量积的几何意义:
数量积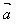 ·
·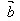 等于
等于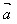 的长度│
的长度│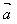 │与
│与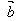 在
在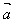 的方向上的投影│
的方向上的投影│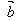 │cosθ的乘积。
│cosθ的乘积。
4.两个向量的数量积的性质:
设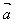 、
、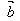 两个非零向量
两个非零向量
(1)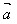 ⊥
⊥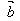 ←→
←→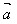 ·
·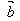 =0
=0
(2)当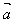 与
与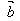 同向时,
同向时,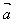 ·
·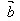 =│
=│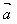 ││
││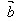 │
│
当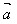 与
与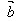 反向时,
反向时,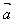 ·
·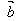 =-│
=-│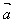 ││
││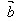 │
│
特别地,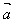 ·
·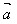 =│
=│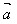 │2或│
│2或│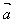 │=√
│=√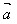 ·
·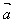
(3)│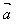 ·
·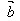 │≤│
│≤│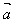 ││
││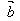 │
│
(4)cosθ=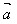 ·
·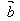 /│
/│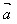 ││
││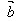 │
│
(5)平面向量数量积的运算律:
已知向量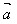 、
、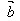 、
、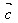 和实数λ,则
和实数λ,则
(1)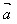 ·
·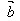 =
=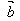 ·
·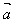 (交换律)
(交换律)
(2)(λ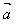 )·
)·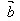 =λ(
=λ(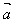 ·
·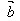 )=
)=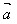 ·(λ
·(λ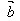 )(数乘结合律)
)(数乘结合律)
(3)(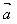 +
+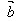 )·
)·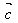 =
=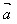 ·
·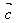 +
+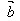 ·
·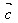 (分配律)
(分配律)