课程内容

《平面向量的基本定理及坐标表示（1）》
教学目标
（1）了解平面向量基本定理；理解平面向量的坐标的概念；
（2）理解平面里的任何一个向量都可以用两个不共线的向量来表示，初步掌握应用向量解决实际问题的重要思想方法；
（3）能够在具体问题中适当地选取基底，使其他向量能够用基底来表达。
教学重点：
平面向量基本定理。
教学难点：
平面向量基本定理的理解与应用。
向量的坐标表示的理解及运算的准确性。
复习引入
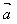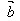如图，有非零向量向量，则与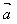共线的条件是什么？

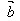向量与非零向量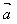共线条件是：
有且只有一个实数λ，使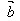=λ.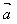
思考：
给定平面内两个向量（→，e₁），（→，e₂），请你作出向量3（→，e₁）+2（→，e₂），（→，e₁）-2（→，e₂）.
平面向量基本定理：
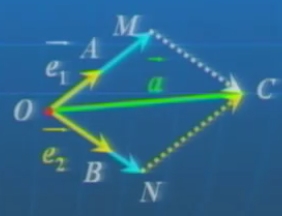
观察如图三个不共线向量（→，e₁）、(→，a)、（→，e₂），它们之间会有怎样的关系呢？
将三个向量的起点移到同一点：

归纳：
根据向量共线的条件，存在唯一的一对实数γ₁，γ₂使得：（→，OM）=γ₁（→，e₁)，（→，ON）=γ₂（→，e₂)故（→，a）=γ₁（→，e₁)+γ₂（→，e₂).
 
想一想：
确定一对不共线向量（→，e₁)，（→，e₂)后，是否平面内任意一个向量都可以用γ₁（→，e₁)+γ₂（→，e₂)来表示呢？
平面向量基本定理：
如果（→，e₁)，（→，e₂)是同一个平面内两个不共线的向量，那么对这一平面内任意一个向量（→，a），有且只有一对实γ₁，γ₂数，使（→，a）=γ₁（→，e₁)+γ₂（→，e₂).
其中（→，e₁)，（→，e₂)叫做表示这一平面内所有向量的一组基底。
问题一：
在刚才我们总结的定理中，基底（→，e₁)，（→，e₂)是不是唯一的呢？
问题二：
给定基底（→，e₁)，（→，e₂)之后，任意一个向量（→，a）的表示是不是唯一的呢？
定理的应用：
例1.如图，已知向量（→，e₁）、（→，e₂），求作向量（→，a），使（→，a）=-2（→，e₁）+3（→，e₂）解：。

例2：如图，（→，OA）、（→，OB）不共线，且（→，AP）且（→，AP）=t（→，AB）（t∈R），用（→，OA），（→，OB）表示（→，OP）.
本体的实质是：
已知O、A、B三点不共线，若点P在直线AB上，则（→，OP）=m（→，OA）+n（→，OB），且m+n=1.
向量的夹角：
已知两个非零向量（→，a）、（→，b），作（→，OA）=（→，a），（→，OB）=（→，b），则∠AOB=θ，叫向量（→，a）、（→，b）的夹角.
当θ=0°，（→，a）、（→，b）同向；
当θ=180°，（→，a）、（→，b）反向；
当θ=90°，（→，a）、（→，b）垂直，记作（→，a）⊥（→，b）.
平面向量的坐标表示
在平面坐标系内，我们分别取与x轴、y轴方向相等的两个单位向量（→，i），（→，j）作为基底，由平面向量基本定理可知，对任何一向量（→，a），有且只有一对实数x、y使得（→，a）=x（→，i）+y（→，j）.
我们把（x，y）叫做向量（→，a）的直角坐标，记作（→，a）=（x，y）.其中x叫做（→，a）在x轴上的坐标x，y叫做（→，a）在y轴上的坐标，（→，a）=（x，y）叫做向量（→，a）的坐标表示。
平面向量的坐标表示
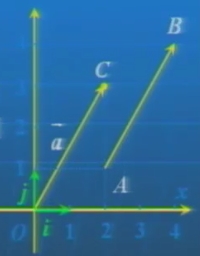
（1）如图，若|（→，i）|=|（→，j）|=1，以向量（→，i）、（→，j）为基底表示向量（→，a）.
（→，a）=2（→，i）+3（→，j）即（→，a）=（2，3）
（2）如图，平面内有A、B两点，能否用坐标来表示向量（→，AB）呢？
（→，AB）=（→，OB）-（→，0A）
=（4（→，i）+4（→，j））-2（（→，i）+1（→，j））
=（4-2）（→，i）+（4-1）（→，j）=2（→，i）+3（→，j）即：（→，AB）=（2,3）

应用：
例3.如图，用基底（→，i）(→，j)分别表示向量（→，a）、（→，b）、（→，c）、（→，d），并求出他们的坐标.