课程内容：

《向量减法运算及其几何意义》
教学目标：
1.了解相反向量的概念；
2.掌握向量的剑法，会作两个向量的减向量，并理解其几何意义。
3.通过阐述向量的减法运算可以转化成向量的加法运算，使学生理解事物间可以相互转化的辩证思想。
教学重点：向量减法的概念和向量减法的作图法。
教学难点：减法运算时方向的确定。
复习回顾：1.向量加法的三角形法则
    2.向量加法的四边形法则
探究：1.向量是否有减法？
      2.向量的减法是否与数的减法有类似的法则？
1.相反向量：与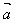长度相等，方向相反的向量，叫做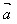的相反向量，记作-。
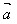（1）-（-）=
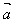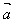
（2）任一向量与其相反向量的和是零向量，即：+（-）=（-）+=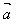
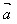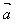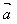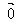
（3）如果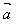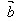，是互为相反的向量，则：=-，=-，+=
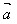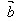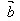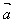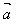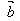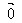
2.向量的减法：
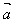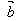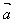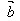    向量加上的相反向量，叫做和的差。
    即-=+（-）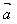
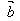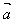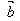思考：（1）（-）+=？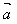
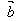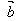（2）已知向量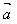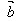，，如何表示图中用红线表示的向量？
向量减法法则：两向量起点相同，则差向量就是连结两向量终点，指向被减向量终点的向量。
注意：（1）起点相同；
（2）指向被减向量的终点。
例1.如图，已知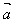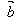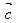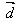向量、、、，求作向量-，-。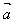
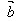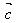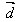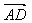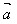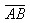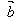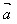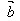例2.如图，平行四边形ABCD中，=，=，用、表示向量、。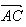
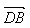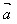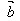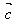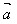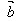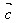例3.如图，已知一点O到平行四边形ABCD的三个顶点A、B、C的向量分别为、、，试用向量、、表示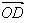。