课程内容：

《向量加法运算及其几何意义》
教学目标：
1.掌握向量的加法运算，并理解其几何意义。
2.会用向量加法的三角形法则和平行四边形法则作两个向量的和向量，培养数形结合解决问题的能力。
3.通过将向量运算与熟悉的数的运算进行类比，使学生掌握向量加法运算的交换律和结合律，并会用它们进行向量计算，渗透类比的数学方法。
教学重点：会用向量加法的三角形法则和平行四边形法则作两个向量的和向量。
教学难点：理解向量加法的定义。
向量的定义以及有关概念
    向量是既有大小又有方向的量。长度相等、方向相同的向量相等，因此，我们研究的向量是与起点无关的自由向量，即任何向量可以在不改变它的方向和大小的前提下，移到任何位置。
问题：数可进行加法运算：1+2=3，那么向量的加法是怎样定义的？长度是1的向量与长度是2的向量相加是否一定是长度为3的向量呢？
（1）某人从A到B，再从B按原方向到C，则两次的位移和：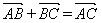
（2）若上题改为从A到B，再从B按反方向到C，则两次的位移和：
（3）某人从A到B，再从B改变方向到C，则两次的位移和：
1.向量的加法：
    求两个向量和的运算，叫做向量的加法。
2.三角形法则：
练习：化简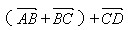
思考：如果三个向量相加，四个向量相加……n个向量相加，和向量又如何？
    将n个向量首尾相接，以第一个向量的起点为起点，最后一个向量的终点为中点的向量，即为这n个向量的和向量。
探究：
（1）两向量的和雨两个数的和有什么关系？
例1.已知向量图3，图4，请使用平行四边形法则作向量+。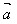
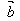    加法的交换律和平行四边形法则
    （1）向量加法的平行四边形法则（对于两个向量共线不适应）
    （2）向量加法的交换律：+=+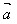
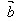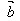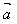
4.你能证明向量加法的结合律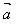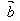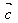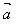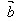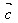：（+）+=+（+）吗？
例2.长江两岸之间没有大桥的地方，常常通过轮渡进行运输，如图所示，一艘船从长江南岸A点出发，以5km/h的速度向垂直于对岸的方向行驶，同时江水的速度为向东2km/h。
（1）试用向量表示江水速度、船速以及船实际航行的速度（保留两个有效数字）；
（2）求船实际航行的速度的大小与方向（用江水速度间的夹角表示，精确到度）。