【此视频课程与人教版第15课的知识点相同，同样适用于华师大第13课，敬请放心学习。】

课程内容：

《因式分解复习》
一、知识点整理
    概念   方法    步骤    应用
    方法：①提取公因式法；②运用公式法；③十字相乘法；④分组分解法
    步骤：一、提  二、套  三、十字  四、分组  五、查
三.分解因式过程中应注意的几个问题：
（1）分解因式总是在指定的数集中进行，不作特别的说明，一般指实数范围内进行；
（2）分解因式的结果是几个整式积的形式，而每一个因式都应分解到不能分解为止；
（3）在提取公因式时，要防止出现提取不尽、提取全项后，得该项为零、提取系数为负的因式疏忽变号等错误；
（4）运用公式法应当注意，当平方项不是一个字母或数时，可用“换元法”进行分解因式。
因式分解公式：
    ma+mb+mc=m(a+b+c)
    a²-b²=(a+b)(a-b)
    a²±2ab+b²=(a±b)²
    x²+(p+q)x+pq=(x+p)(x+q)
练习：
1.下列由左到右的变形是因式分解的是（   ）
    A.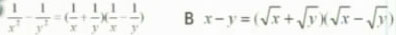
    C.（3x+y）（3x-y）=9x²-y²   D.4x²-1=（2x+1）（2x-1）
2.下列因式分解正确的是：（    ）
    A.ab-a-b+1=(a-1)(b-1)      B.a⁴-b²=(a2+b)(a2-b)
    C.x²-3x-4=(x+2)(x-2)       D.3x³+2x²+x=x(3x²+2x)
算一算：
    1.分解因式
（1）-x²-2x；  （2）ax²+4ay²+4axy；  （3）a²（x-y）+（y-x）³；
（4）4x²-y²-2y-1；  （5）3x²-4√3x+3
    2.（1）2005²-2005×2006=
      （2）
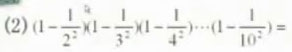
    3.若m-n=6，mn=7，则mn²-m²n的值是_____________________。
      若x²+xy=2，y²+xy=7，则x²-y²=____________________。
    4.已知正整数x、y满足x²-12=y²，则x+y的值是_______________。
四、因式分解的应用
1.观察图形，根据图形的面积关系，不需要其他的线，便可以得到一个用来分解因式的公式，这个公式是______________________________。
2.在边长为a的正方形中挖掉一个边长为b的小正方形，把余下的部分剪拼成一个矩形，通过计算这两个图形的面积，验证了一个等式，则这个等式是（    ）
    A.a²-b²=（a+b）（a-b）      B.（a+b）²=a²+2ab+b²
    C.（a-b）²=a²-2ab+b²        D.（a+2b）（a-b）=a²+ab-2b²
3.如图，用4张全等的矩形纸片拼成的图形，请利用图中空白部分的面积的不同表示方法写出一个关于a、b的恒等式。
4.阅读下面因式分解的过程，再回答所提出的问题：
    1+x+x（x+1）+x（x+1）²=（1+x）[1+x+x（x+1）]=（1+x）²（1+x）=（1+x）³
（1）上述分解因式的方法是____________，共应用了________次；
（2）若分解1+x+x（x+1）+x（x+1）²+…+x（x+1）²⁰⁰⁵，则应用上述方法____________次，结果是___________________；
（3）分解因式：1+x+x（x+1）+x（x+1）²+…+x（x+1）ⁿ（n为正整数）。
6.请你给代数式x²+4加上一个单项式后，使它能成为一个整式的平方，请你写出所有符合条件的单项式。
7.请写出一个三项式，使它能先提取公因式，再运用公式法来分解，你编写的三项式是_______________，分解因式的结果是_____