课程内容

《直线与平面、平面与平面的位置关系》
探究（一）直线与平面之间的位置关系
问题：如图，线段A′B所在直线与长方体ABCD-A′B′C′D′的六个面所在的平面有几种位置关系？
思考1：通过上面的观察和分析，直线与平面有三种位置关系，即直线在平面内，直线与平面相交，直线与平面平行。这些位置关系的基本特征是什么？
（1）直线在平面内——有无数个公共点；
（2）直线与平面相交——有且只有一个公共点；
（3）直线与平面平行——没有公共点。
思考2：下图表示直线与平面的三种位置，如何用符号语言描述这三种位置关系？
直线在平面内    直线与平面相交    直线与平面平行
a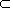α        a∩α=P            a∥α
思考6：直线与平面相交或平行的情况统称为直线在平面外，用符号语言怎样表述？
a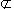α
思考3：过平面外一点可作多少条直线与这个平面平行？若直线l平行于平面α，则直线l与平面α内的直线的位置关系如何？
思考4：若两条平行直线中有一条平行于一个平面，那么另一条也平行与这个平面吗？
探究（二）平面与平面之间的位置关系
问题：如图，围成长方体ABCD-A′B′C′D′的六个面，两两之间的位置关系有几种？
思考1：由上面的观察和分析可知，两个平面的位置关系只有两种，即两个平面平行，两个平面相交。这两种位置关系的基本特征是什么？
（1）两个平面平行——没有公共点；
（2）两个平面相交——有一条公共直线。
思考2：下图表示两平面之间的两种位置，如何用符号语言描述这两种位置关系？
两个平面平行    两个平面相交
  α∥β          α∩β=l
思考3：已知平面α，β和直线a，b，且α∥β，a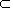α，b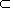β，则直线a与平面β的位置关系如何？直线a与直线b的位置关系如何？
理论迁移
例1：给出下列四个命题：
（1）若直线l上有无数个点不在平面α内，则l∥α。
（2）若直线l与平面α平行，则l与平面α内的任意一条直线都平行。
（3）若直线l与平面α平行，则l与平面α内的任意一条直线都没有公共点。
（4）若直线l在平面α内，且l与平面β平行，则平面α与平面β平行。
其中正确命题的个数共有______个。
例2：如图，正方体ABCD-A′B′C′D′的棱长为8，M，N，P分别是A′B′，AD，BB′的中点。
（1）画出过点M，N，P的平面与平面ABCD的交线以及与平面BB′C′C的交线；
（2）设平面PMN与棱BC交于点Q，求PQ的长。