课程内容:
《直线、平面平行的判定》
问题提出:1.直线与平面的位置关系有哪几种?
平行、相交、在平面内。
2.在直线与平面的位置关系中,平行是一种非常重要的关系,它是空间线面位置关系的基本形态,那么怎样判定直线与平面平行呢?
知识探究(一):直线与平面平行的判定定理:
思考1:生活中,我们注意到门扇的两边是平行的,当门扇绕着一边转动时,观察门扇转动的一边l与门框所在平面的位置关系如何?
思考2:若将一本书平放在桌面上,翻动书的封面,观察封面边缘所在直线l与桌面所在的平面具有怎样的位置关系?
思考3:如图,设直线b在平面α内,直线a在平面α外,猜想在什么条件下直线a与平面α平行。
思考4:如果直线a与平面α内的一条直线b平行,则直线a与平面α一定平行吗?
思考5:设直线b在平面α内,直线a在平面α外,若a∥b,则直线a与直线b确定一个平面β,那么平面α与平面β的位置关系如何?此时若直线a与平面α相交,则交点在何处?
定理:若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
思考6:上述定理通常称为直线与平面平行的判定定理,该定理用符号语言可怎样表述?
a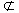 α,b
α,b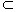 α,且a∥b
α,且a∥b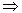 a∥α
a∥α
思考7:直线与平面平行的判定定理可简述为“线线平行,则线面平行”,在实际应用中它有何作用?
通过直线间的平行,推证直线与平面平行,即将直线与平面的平行关系(空间问题)转化为直线间的平行关系(平面问题)。
思考8:设直线a,b为异面直线,经过直线a可作几个平面与直线b平行?过b外一点P可作几个平面与直线a,b都平行?
例1.在空间四边形ABCD中,E,F分别为AB,AD的中点,求证:EF∥平面BCD。
例2.在长方体ABCD—A1B1C1D1中,(1)作出过直线AC且与直线BD1平行截面,并说明理由。(2)设E,F分别是A1B和B1C的中点,求证直线EF∥平面ABCD。
问题提出:1.空间两个不同平面的位置关系有哪几种情况?
2.两个平面平行的基本特征是什么?有什么简单办法判定两个平面平行呢?
知识探究(一):平面与平面平行的判定定理:
思考1:根据定义,判定平面与平面平行的关键是什么?
思考2:三角板的一条边所在直线与桌面平行,这个三角板所在平面与桌面平行吗?
思考3:三角板的两条边所在直线分别于面平行,三角板所在平面与桌面平行吗?
思考4:一般地,如果平面α内有一条直线平行于平面β,那么平面α与平面β一定平行吗?如果平面α内有两条直线平行于平面β,那么平面α与平面β一定平行吗?
思考5:设a,b是平面α内的两条相交直线,且a∥β,b∥β,在此条件下,若α∩β=l,则直线a、b与直线l的位置关系如何?
思考6:上述定理通常称为平面与平面平行的判定定理,该定理用符号语言课怎样表述?
a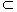 α,b
α,b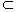 α,a∩b=P,且a∥β,b∥β
α,a∩b=P,且a∥β,b∥β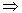 α∥β
α∥β
思考7:在直线与平面平行的判定定理中,“a∥β,b∥β”,可用什么条件代替?由此可得什么推论?
推论:如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行。
例3.在正方体ABCD—A'B'C'D'中,求证:平面AB'D'∥平面BC'D。
例4.在三棱锥P—ABC中,点D、E、F分别是△PAB、△PBC、△PAC的重心,求证:平面DEF∥平面ABC。
此内容正在抓紧时间编辑中,请耐心等待
孙老师
男,中教高级职称
在教学中勤恳敬业,教学成绩优异,多次被评为“优秀数学教师”称号。
























