课程内容:
《函数的表示法(1)》
提问思考:下列3题分别是函数的哪种表示法及它们的定义是什么?
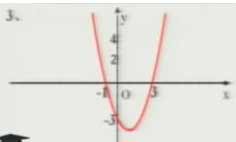
1.y=x2-2x-3
2.
3.
1.解析式:就是用数学表达式表示两个变量之间的对应关系。
2.列表法:用列出表格来表示两个变量的函数关系。
3.图象法:用函数图象表示两个变量之间的对应关系。
例1.某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元。你能用函数的三种表示法表示函数y=f(x)吗?
三种表示方法的特点:
解析法的特点:简明、全面地概括了变量间的关系;可以通过用解析式求出任意一个自变量所对应的函数值。
列表法的特点:不通过计算就可以直接看出与自变量的值相对应的函数值。
图象法的特点:直观形象地表示出函数的变化情况,有利于通过图形研究函数的某些性质。
三种表示方法举例:
(1)解析法:y=kx(k≠0),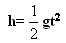
(2)列表法:
(3)图象法: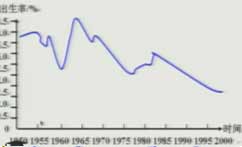
例2.下表是某校高一(1)班三位同学在高一学年度几次数学测试的成绩及班级平均分表:设测试序号为X,成绩为Y。每位同学的成绩Y与测试序号X之间的函数关系能用解析法表示吗?
例3.画出函数y=│x│的图像。
例4.已知函数y=│x+1│+│x-3│,画出它的图像及求这个函数的定义域和值域。
例5.某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里按5公里计算)。如果某条线路的总里程为20公里,请根据题意,写出票价y与里程x之间的函数解析式,并画出函数的图象。
注意:1.有些函数在它的定义域中,对于自变量x的不同取值范围,对应关系不同,这种函数通常称为分段函数。分段函数的表达式虽然不止一个,但它不是几个函数,而是一个函数。
2.函数图象不一定是光滑的曲线(直线),还可以是一些孤立的点,一些线段,一段曲线等。
练习:
1.某质点在30s内运动速度ccm/s是时间t的函数,它的图象如下图。用解析式表示出这个函数,并求出9s时质点的速度。
2.以下叙述正确的有( )
(1)分段函数的定义域是各段定义域的并集,值域是各段值域的并集。
(2)分段函数在定义域的不同部分有不同的对应法则,但它是一个函数。
(3)若D1、D2分别是分段函数的两个不同对应法则的值域,则D1∩D2≠φ也能成立。
A.1个 B.2个 C.3个 D.0个
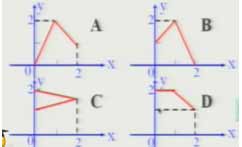
3.设A=[0,2],B=[1,2],在下列各图中,能表示f:A→B的函数是( )