课程内容：

《圆的一般式方程》
圆的标准方程：（x-a）²+（y-b）²=r²
把它展开得到：x²+y²-2ax-2by+a²+b²-r²=0
任何圆的方程都可以通过展开化成形如：
x²+y²+Dx+Ey+F=0的方程 ①
请大家思考一下：形如x²+y²+Dx+Ey+F=0的方程的曲线是不是圆？
将①配方法，得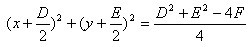： ②
（1）当D²+E²-4F＞0时，②表示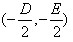以为圆心，以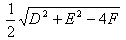为半径的圆；此时①称作圆的一般方程。
即称形如x²+y²+Dx+Ey+F=0（D²+E²-4F＞0）的方程为圆的一般方程。
（2）当D²+E²-4F=0时，方程②表示一个点；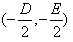
思考：我们学习了圆的一般方程和圆的标准方程，请大家比较这两种方程，并归纳它们各自的特点？
（1）圆的标准方程带有明显的几何的影子，圆心和半径一目了然；
（2）圆的一般方程表现出明显的代数的形式与结构，更适合方程理论的运用。
例1.求过三点O（0,0），M₁（1,1），M₂（4,2）的圆的方程，并求这个圆的半径长和圆心坐标。
求圆的方程常用“待定系数法”，用“待定系数法”求圆的方程的大致步骤是：
①根据题意，选择标准方程或一般方程；
②根据条件列出关于a，b，r或者D，E，F的方程组；
③解出a，b，r或D，E，F，代入标准方程或一般方程。
关于何时设圆的标准方程，何时设圆的一般方程：一般说来，如果由已知条件容易求圆心的坐标、半径或需要用圆心的坐标、半径列方程的问题，往往设圆的标准方程；如果已知条件和圆心坐标或半径都无直接关系，往往设圆的一般方程。
例2.求圆心在直线l：x+y=0上，且过两圆C₁：x²+y²-2x+10y-24=0，C₂：x²+y²+2x+2y-8=0的交点的圆的方程。
练习：
1.求下列各圆的一般方程：
（1）过点A（5,1），圆心在点C（8，-3）
（2）过三点A（-1,5），B（5,5），C（6，-2）