课程内容:
《两点间的距离》
已知平面上两点P1(x1,y1),P2(x2,y2),如何求P1P2的距离|P1P2|呢?
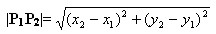
特别地,原点O与任一点的P(x,y)的距离:
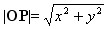
练习:1.求下列两点间的距离:
(1)A(6,0),B(-2,0);(2)C(0,-4),D(0,-1);(3)P(6,0),Q(0,-2);(4)M(2,1),N(5,-1)
例3.已知点A(-1,2),B(2,√7),在x轴上求一点P,使得|PA|=|PB|,并求|PA|的值。
练习:2.求在x轴上与点A(5,12)的距离为13的坐标。
3.已知点P的横坐标是7,点P与点N(-1,5)间的距离等于10,求点P的纵坐标。
例4.证明平行四边形四条边的平方和等于两条对角线的平方和。
总结:用坐标法证明简单的平面几何问题的步骤:
第一步:建立坐标系,用坐标系表示有关的量;
第二步:进行有关的代数运算;
第三步:把代数运算结果“翻译”成几何关系。
练习:4.证明直角三角形斜边的中点到三个顶点的距离相等。
此内容正在抓紧时间编辑中,请耐心等待
岳老师
男,中教高级职称
执教以来,一直担任数学教学工作。在工作中注重对教学方法的探索,对教育方式的研究。