课程内容:
《两条直线的交点坐标》
思考:已知两条直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,相交,如何求这两条直线交点的坐标?
用代数方法求两条直线的交点坐标,只需写出这两条直线的方程,然后联立求解。
一般地,将两条直线的方程联立,得方程组
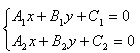
若方程组有唯一解,则两条直线相交,此解就是交点坐标;若方程组无解,则两条直线无公共点,此时两条直线平行。
例1.求下列两条直线的交点坐标:l1:3x+4y-2=0,l2:2x+y+2=0。
探究:当λ变化时,方程3x+4y-2+λ(2x+y+2)=0表示什么图形?图形有何特点?
例2.判断下列各对直线的位置关系,如果相交,求出交点坐标。
(1)l1:x-y=0,l2:3x+3y-10=0;(2)l1:3x-y+4=0,l2:6x-2y=0;(3)l1:3x+4y-5=0,l2:6x+8y-10=0
课后练习:1.直线5x+4y=2m+1与2x+3y=m交与第四象限,则m的取值范围是______。
2.已知A(0,0),B(3,0),C(1,2),则△ABC的垂心坐标是______,外心坐标是______。
3.求直线x-y-5=0,2x+y-7=0,4x-y-11=0所围成的三角形的面积。
4.已知两点A(1,4),B(3,1),直线L:kx+2与线段AB相较于A、B之间,则k的取值范围是______。









